Problem of The Day: Lowest Common Ancestor of Deepest Leaves

Problem Statement

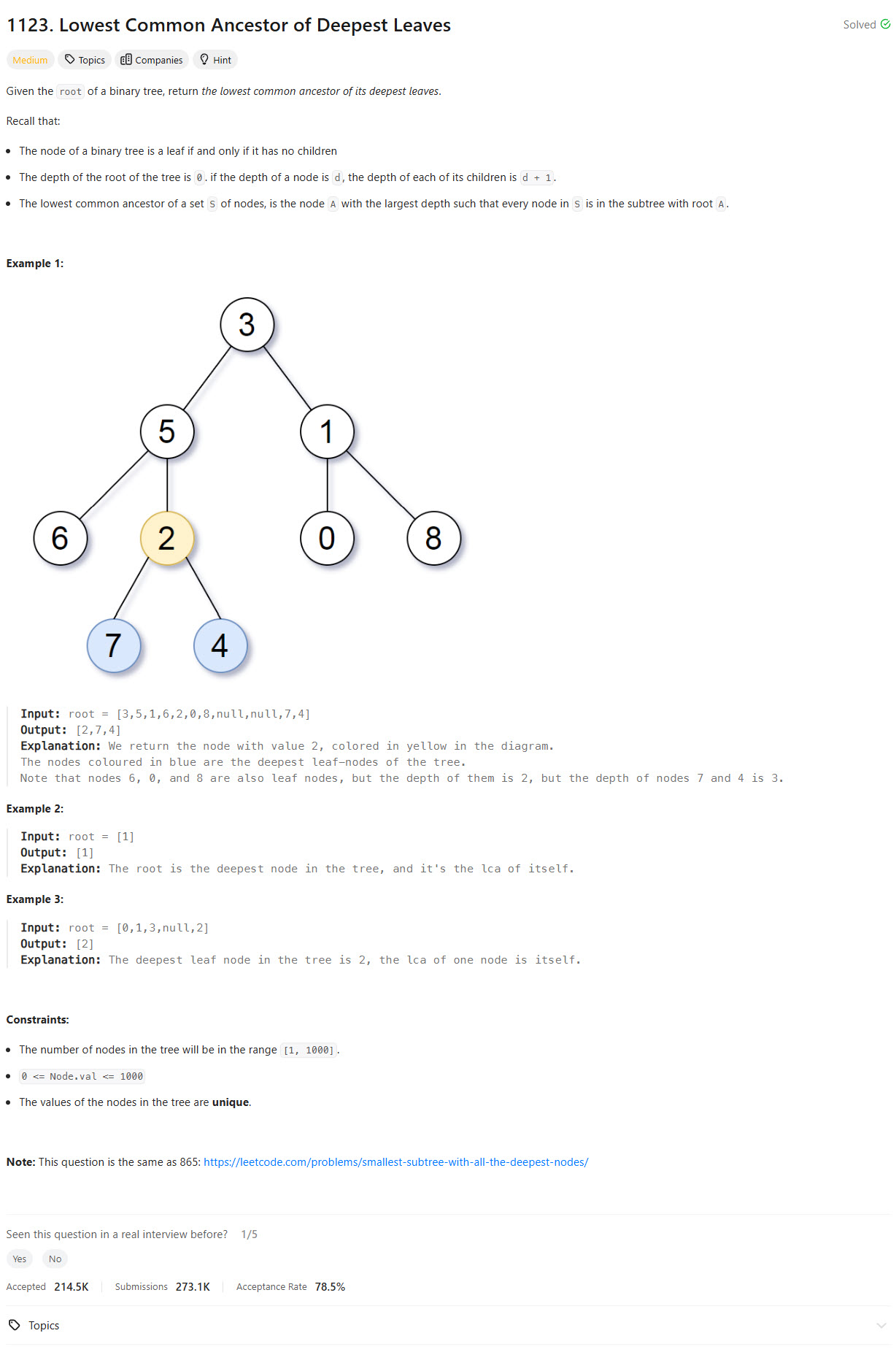
Intuition

To find the Lowest Common Ancestor (LCA) of the deepest leaves in a binary tree, we need to:

1. Determine how deep the deepest leaves go.
2. Collect all leaves at that deepest level.
3. Find the lowest node in the tree that is an ancestor to all of those deepest leaves.

Approach

1. Calculate the maximum depth of the tree using a recursive function find_depth.

   • This function returns the depth of the deepest subtree by recursively exploring left and right branches.

2. Collect all deepest leaves using find_deepest_leaves.

   • Traverse the tree while tracking the current level.
   • When the current level matches the maximum depth, add the node to a list of deepest leaves.

3. Find the LCA of the deepest leaves:

   • If there is only one deepest leaf, it is its own ancestor — return it.
   • Otherwise, use a recursive lca function that checks whether each subtree contains one of the target leaves.
   • When two of the three flags (left, right, mid) are True, the current node is the LCA.
   • Save the LCA in self.lca_node.

Complexity

• Time complexity:
  \(O(n)\)
  Each of the three main functions (find_depth, find_deepest_leaves, and lca) traverses the tree once.

• Space complexity:
  \(O(h)\)
  Where ( h ) is the height of the tree due to recursive stack space.

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def lcaDeepestLeaves(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        res = []
        depth = [0]

        def find_depth(node):
            if not node:
                return -1
            left = find_depth(node.left) + 1
            right = find_depth(node.right) + 1
            return max(left, right)

        def find_deepest_leaves(node, last_level, curr_level, leaves):
            if not node:
                return
            if curr_level == last_level:
                leaves.append(node)
                return
            find_deepest_leaves(node.left, last_level, curr_level + 1, leaves)
            find_deepest_leaves(node.right, last_level, curr_level + 1, leaves)

        def lca(node, p, q):
            if not node:
                return False

            left = lca(node.left, p, q)
            right = lca(node.right, p, q)
            mid = node is p or node is q
            if sum([left, right, mid]) >= 2:
                self.lca_node = node
            return left or right or mid

        deepest_level = find_depth(root)
        leaves = []
        find_deepest_leaves(root, deepest_level, 0, leaves)
        if len(leaves) == 1:
            return leaves[0]

        self.lca_node = root
        lca(root, leaves[0], leaves[-1])
        return self.lca_node

Editorial

Approach 1: Recursion

class Solution:
    def lcaDeepestLeaves(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        def dfs(root):
            if not root:
                return 0, None

            left = dfs(root.left)
            right = dfs(root.right)

            if left[0] > right[0]:
                return left[0] + 1, left[1]
            if left[0] < right[0]:
                return right[0] + 1, right[1]
            return left[0] + 1, root

        return dfs(root)[1]