Problem of The Day: Number of Sub-arrays With Odd Sum

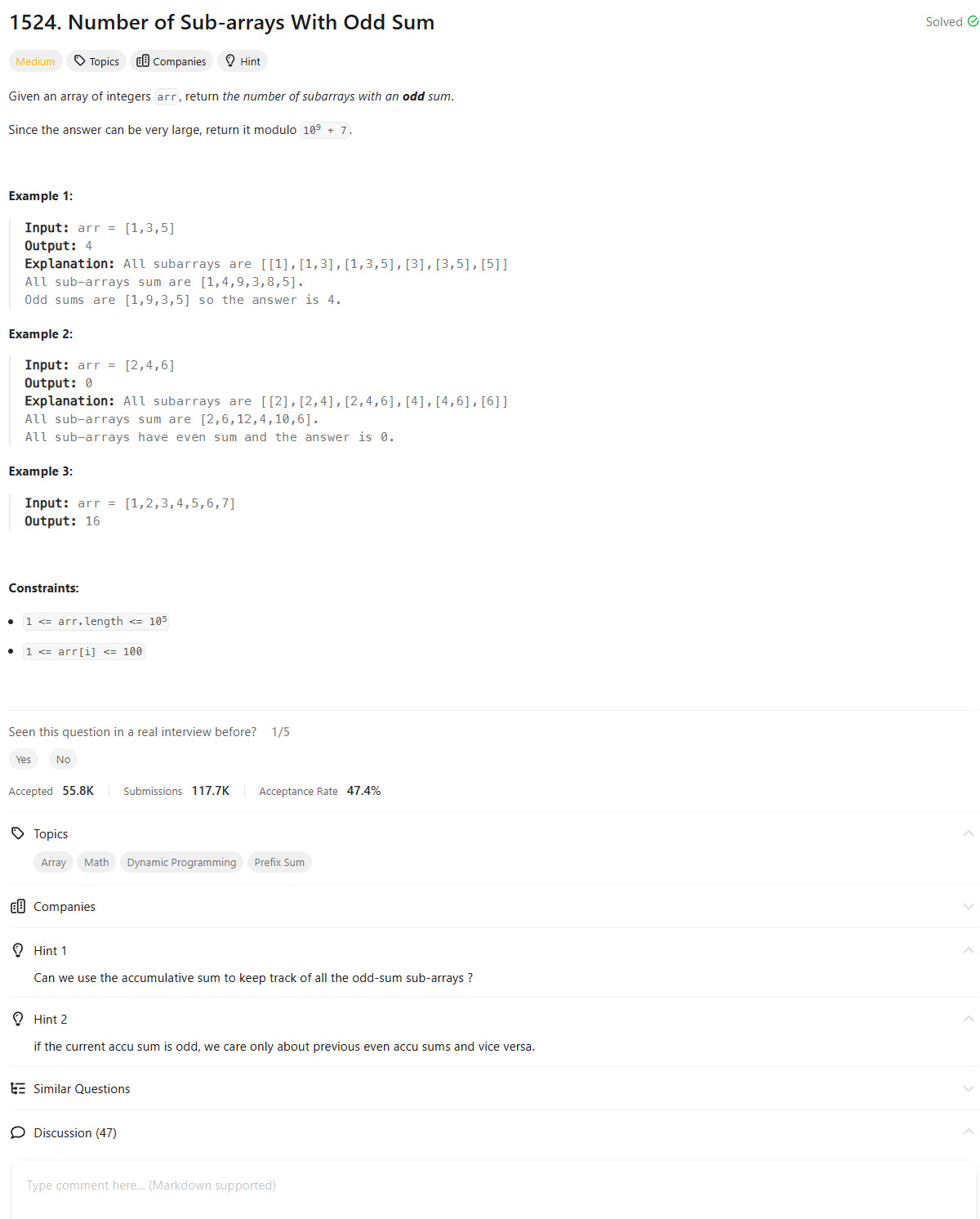
Problem Statement

Prefix Sum Approach

class Solution:
    def numOfSubarrays(self, arr: List[int]) -> int:
        N = len(arr)
        curr = 0
        res = 0
        even = 1 # since start at 0 even
        odd = 0
        MOD = 10**9 + 7
        for i, x in enumerate(arr):
            curr += x
            if curr % 2 == 0:
                even += 1
                res += odd
            else:
                odd += 1
                res += even

            res %= MOD
        return res

Editorial

Approach 1: Brute Force (TLE)

class Solution:
    def numOfSubarrays(self, arr: List[int]) -> int:
        MOD = 1e9 + 7
        n = len(arr)
        count = 0

        # Generate all possible subarrays
        for start_index in range(n):
            current_sum = 0
            # Iterate through each subarray starting at start_index
            for end_index in range(start_index, n):
                current_sum += arr[end_index]
                # Check if the sum is odd
                if current_sum % 2 != 0:
                    count += 1

        return int(count % MOD)

Approach 2: Dynamic Programming

class Solution:
    def numOfSubarrays(self, arr: List[int]) -> int:
        MOD = 1e9 + 7
        n = len(arr)

        # Convert elements to 0 (even) or 1 (odd)
        for i in range(n):
            arr[i] %= 2

        # dp_even[i] represents the number of subarrays with an even sum ending
        # at index i. dp_odd[i] represents the number of subarrays with an odd
        # sum ending at index i
        dp_even, dp_odd = [0] * n, [0] * n

        # Initialization based on the last element
        # The last element is even
        if arr[n - 1] == 0:
            dp_even[n - 1] = 1
        else:
            # The last element is odd
            dp_odd[n - 1] = 1

        # Traverse the array in reverse
        for num in range(n - 2, -1, -1):
            if arr[num] == 1:
                # Odd element contributes to odd subarrays
                dp_odd[num] = (1 + dp_even[num + 1]) % MOD
                # Even element continues the pattern
                dp_even[num] = dp_odd[num + 1]
            else:
                # Even element contributes to even subarrays
                dp_even[num] = (1 + dp_even[num + 1]) % MOD
                # Odd element continues the pattern
                dp_odd[num] = dp_odd[num + 1]

        # Sum all the odd subarrays
        count = 0
        for odd_count in dp_odd:
            count += odd_count
            count %= MOD

        return int(count)

Approach 3: Prefix Sum with Odd-Even Counting

class Solution:
    def numOfSubarrays(self, arr: List[int]) -> int:
        MOD = 10**9 + 7
        count = prefix_sum = 0
        # even_count starts as 1 since the initial sum (0) is even
        odd_count = 0
        even_count = 1

        for num in arr:
            prefix_sum += num
            # If current prefix sum is even, add the number of odd subarrays
            if prefix_sum % 2 == 0:
                count += odd_count
                even_count += 1
            else:
                # If current prefix sum is odd, add the number of even
                # subarrays
                count += even_count
                odd_count += 1

            count %= MOD  # To handle large results

        return count