Thomas Ngo

Software Engineer

2 minute read

Problem Statement

problem

Intuition

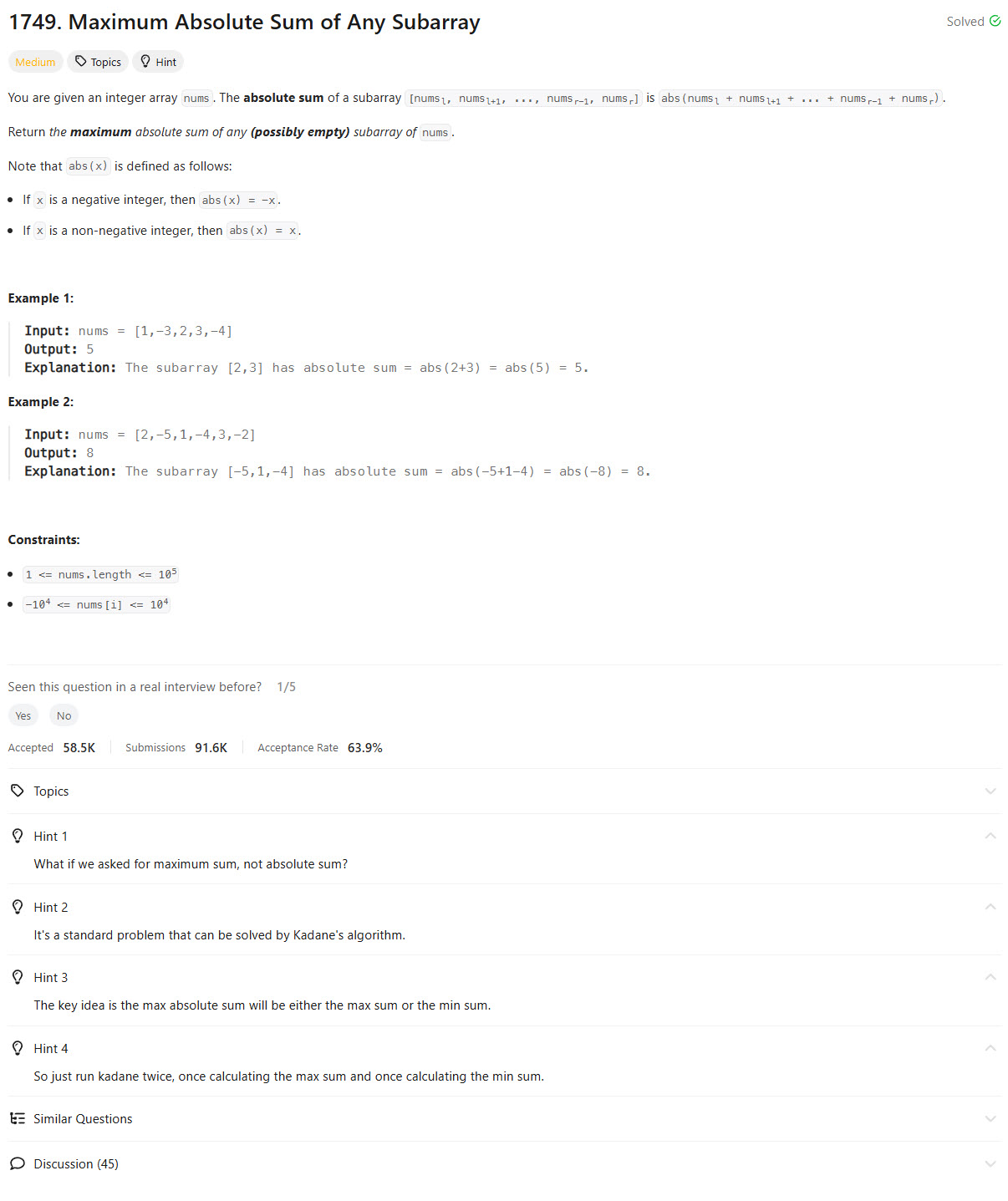
The problem requires finding the maximum absolute sum of any subarray in a given list of integers. The absolute sum is the largest magnitude sum, whether positive or negative.

The key observation is that the maximum absolute sum can come from either the maximum subarray sum (Kadane’s algorithm) or the minimum subarray sum (Kadane’s algorithm applied to the negative of the array). Thus, we track both values and return the maximum absolute value.

Approach

  1. Track Maximum Subarray Sum: Use Kadane’s algorithm to compute the maximum sum of a contiguous subarray. Maintain a running sum and reset to 0 when the sum goes negative.
  2. Track Minimum Subarray Sum: Similarly, track the minimum sum of a contiguous subarray using Kadane’s algorithm but in reverse. Instead of resetting when the sum goes negative, reset when it goes positive.
  3. Compute Absolute Maximum: The answer is the maximum of the absolute values of the maximum and minimum subarray sums.

Complexity

  • Time Complexity:
    • \(O(n)\), since we iterate over the array twice.
  • Space Complexity:
    • \(O(1)\), as we use only a few integer variables for tracking sums.

Code

from typing import List

class Solution:
    def maxAbsoluteSum(self, nums: List[int]) -> int:
        N = len(nums)
        max_sum = float('-inf')
        min_sum = float('inf')
        curr = 0

        # Compute maximum subarray sum (Kadane's algorithm)
        for x in nums:
            curr += x
            if curr < 0:
                curr = 0
            max_sum = max(max_sum, curr)

        curr = 0

        # Compute minimum subarray sum (Kadane's algorithm for negative sum)
        for x in nums:
            curr += x
            if curr > 0:
                curr = 0
            min_sum = min(min_sum, curr)

        return max(max_sum, abs(min_sum))

Editorial

Approach 1: Greedy - Prefix Sum

class Solution:
    def maxAbsoluteSum(self, nums):
        min_prefix_sum = float("inf")
        max_prefix_sum = float("-inf")
        prefix_sum = 0
        max_abs_sum = 0

        for num in nums:
            # Prefix sum from index 0 to i
            prefix_sum += num

            # Minimum & Maximum prefix sum we have seen so far
            min_prefix_sum = min(min_prefix_sum, prefix_sum)
            max_prefix_sum = max(max_prefix_sum, prefix_sum)

            if prefix_sum >= 0:
                # If the prefix_sum is positive, we will get the difference
                # between prefix_sum & min_prefix_sum
                max_abs_sum = max(
                    max_abs_sum, max(prefix_sum, prefix_sum - min_prefix_sum)
                )
            elif prefix_sum <= 0:
                # If the prefix_sum is negative, we will get the absolute difference
                # between prefix_sum & max_prefix_sum
                max_abs_sum = max(
                    max_abs_sum,
                    max(abs(prefix_sum), abs(prefix_sum - max_prefix_sum)),
                )

        return max_abs_sum

Approach 2: Greedy - Prefix Sum - Shorter

class Solution:
    def maxAbsoluteSum(self, nums):
        min_prefix_sum = 0
        max_prefix_sum = 0
        prefix_sum = 0

        for num in nums:
            prefix_sum += num

            min_prefix_sum = min(min_prefix_sum, prefix_sum)
            max_prefix_sum = max(max_prefix_sum, prefix_sum)

        return max_prefix_sum - min_prefix_sum

You may also enjoy