Problem of The Day: Check if Number is a Sum of Powers of Three

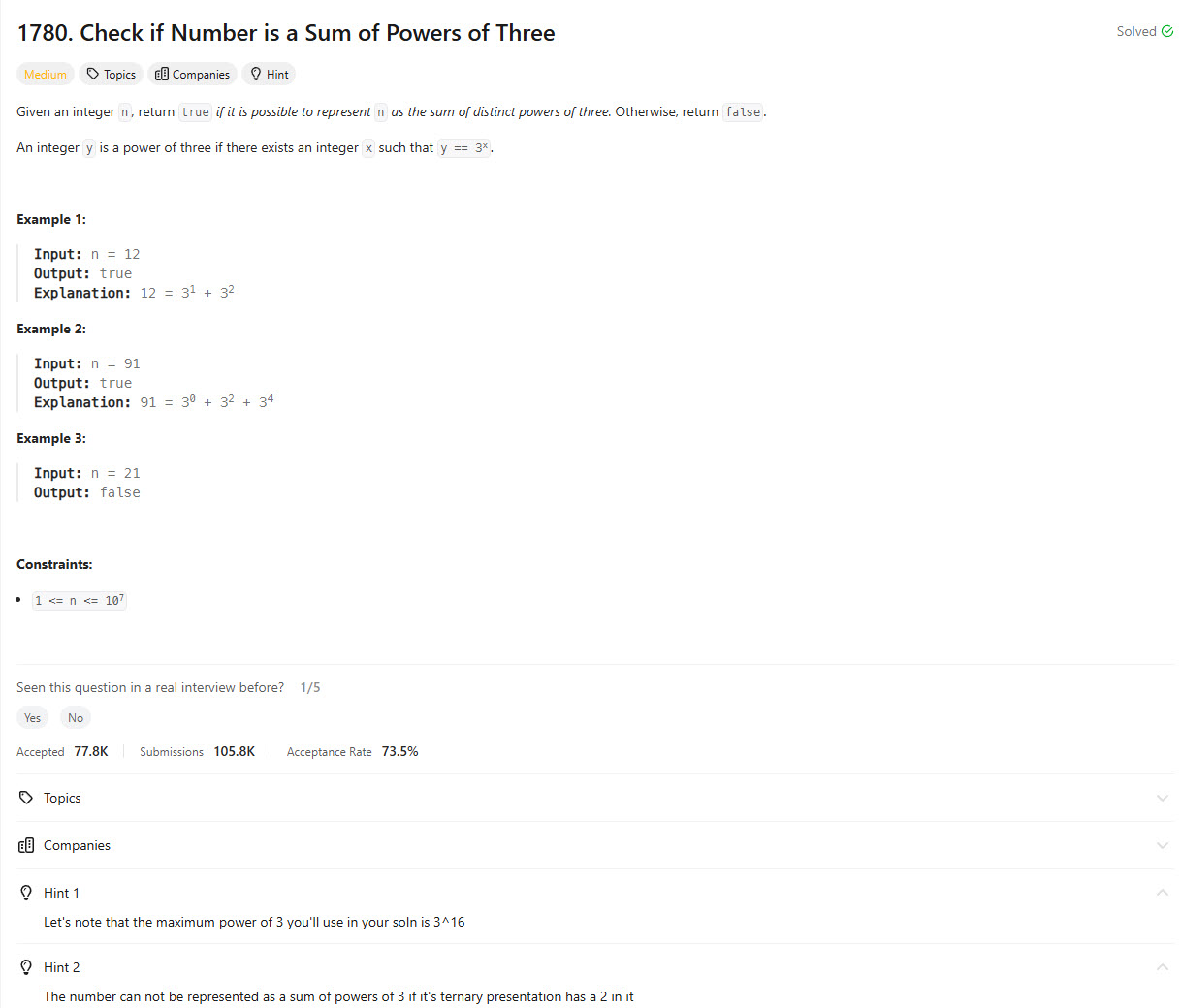
Problem Statement

Brute Force [TLE]

class Solution:
    def checkPowersOfThree(self, n: int) -> bool:
        def dfs(power, target):
            if target == 0:
                return True
            if target < 0:
                return False
            if 3**power > target:
                return False
            include = dfs(power + 1, target - 3**power)
            if include:
                return True
            exclude = dfs(power + 1, target)
            if exclude:
                return True
            return False


        return dfs(0, n)

Approach 1: Backtracking (Brute Force)

class Solution:
    def checkPowersOfThree(self, n: int) -> bool:
        return self._check_powers_of_three_helper(0, n)

    def _check_powers_of_three_helper(self, power: int, n: int) -> bool:
        # Base case: if n becomes 0, we have successfully formed the sum
        if n == 0:
            return True

        # If the current power of 3 exceeds n, we can't use it, so return false
        if 3**power > n:
            return False

        # Option 1: Include the current power of 3 and subtract it from n
        add_power = self._check_powers_of_three_helper(power + 1, n - 3**power)

        # Option 2: Skip the current power of 3 and try with the next power
        skip_power = self._check_powers_of_three_helper(power + 1, n)

        # Return true if either option leads to a valid solution
        return add_power or skip_power

Approach 2: Optimized Iterative Approach

class Solution:
    def checkPowersOfThree(self, n: int) -> bool:
        power = 0

        # Find the largest power that is smaller or equal to n
        while 3**power <= n:
            power += 1

        while n > 0:
            # Subtract current power from n
            if n >= 3**power:
                n -= 3**power
            # We cannot use the same power twice
            if n >= 3**power:
                return False
            # Move to the next lower power
            power -= 1

        # n has reached 0
        return True

Approach 3: Ternary Representation

class Solution:
    def checkPowersOfThree(self, n: int) -> bool:
        while n > 0:
            # Check if this power should be used twice
            if n % 3 == 2:
                return False
            # Divide n by 3 to move to the next greater power
            n //= 3
        # The ternary representation of n consists only of 0s and 1s
        return True