Problem of The Day: Maximum Ascending Subarray Sum

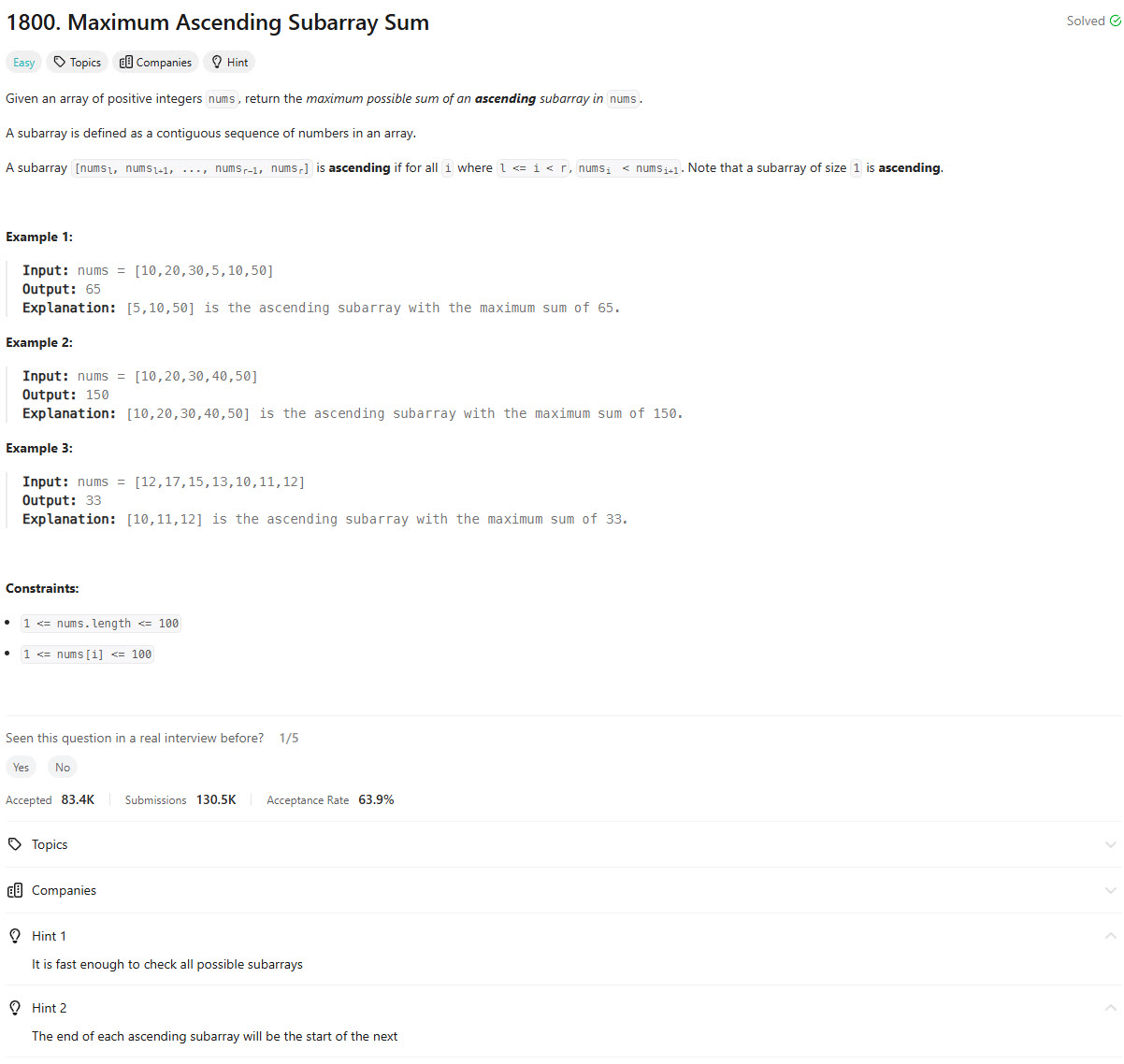
Problem Statement

Prefix Approach [Accepted]

class Solution:
    def maxAscendingSum(self, nums: List[int]) -> int:
        if len(nums) == 1:
            return nums[0]
        l, r = 0, 0
        res = 0
        curr = 0
        N = len(nums)
        prefix = [0] * (N)
        for i in range(N):
            curr += nums[i]
            prefix[i] = curr

        for r in range(1, N):
            res = max(res, nums[l])
            if nums[r - 1] >= nums[r]:
                l = r
            res = max(res, prefix[r] - prefix[l] + nums[l])
        return res

Editorial

Approach 1: Brute-Force

class Solution:
    def maxAscendingSum(self, nums):
        max_sum = 0

        # Outer loop to start from each element in the array
        for start_idx in range(len(nums)):
            current_subarray_sum = nums[start_idx]

            # Inner loop to check the next elements forming an ascending subarray
            end_idx = start_idx + 1
            while end_idx < len(nums) and nums[end_idx] > nums[end_idx - 1]:
                current_subarray_sum += nums[end_idx]
                end_idx += 1

            # Update max_sum if we find a larger ascending subarray sum
            max_sum = max(max_sum, current_subarray_sum)

        return max_sum

• time: O(n^2)
• space: O(1)

Approach 2: Linear Scan

class Solution:
    def maxAscendingSum(self, nums: List[int]) -> int:
        maxSum = 0
        currentSubarraySum = nums[0]

        # Loop through the list starting from the second element
        for currentIdx in range(1, len(nums)):
            if nums[currentIdx] <= nums[currentIdx - 1]:
                # If the current element is not greater than the previous one,
                # update maxSum
                maxSum = max(maxSum, currentSubarraySum)
                # Reset the sum for the next ascending subarray
                currentSubarraySum = 0
            currentSubarraySum += nums[currentIdx]

        # Final check after the loop ends to account for the last ascending
        # subarray
        return max(maxSum, currentSubarraySum)

• time: O(n)
• space: O(1)