Problem of The Day: Minimum Operations to Make a Uni-Value Grid

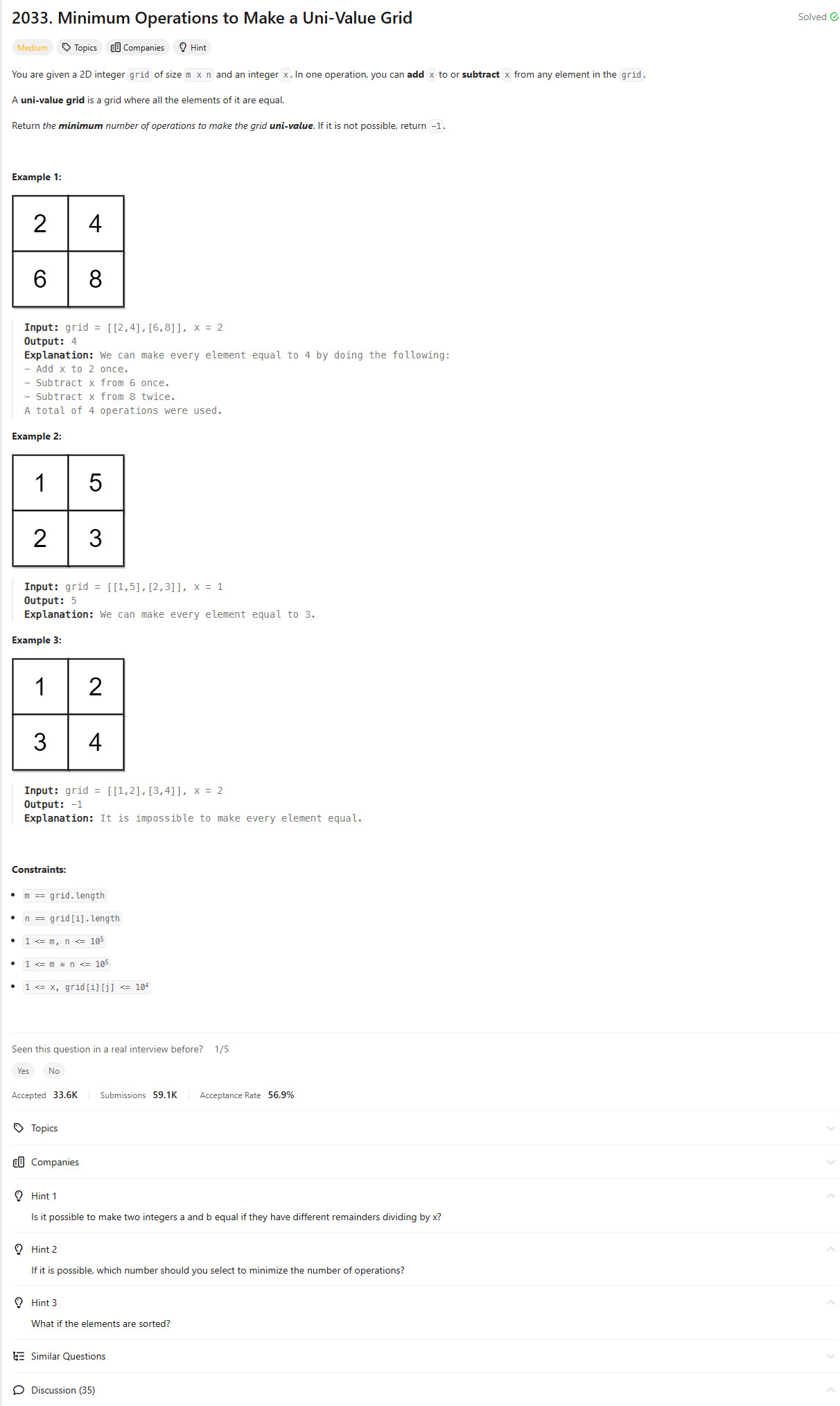
Problem Statement

Solution

class Solution:
    def minOperations(self, grid: List[List[int]], x: int) -> int:
        from sortedcontainers import SortedList
        arr = SortedList()
        n = len(grid)
        m = len(grid[0])
        remainder = grid[0][0] % x
        for row in range(n):
            for col in range(m):
                if grid[row][col] % x != remainder:
                    return -1
                arr.add(grid[row][col])

        N = n * m
        if N % 2 == 0:
            mid = (N // 2) - 1
        else:
            mid = N // 2
        target = arr[mid]
        res = 0
        for i in range(N):
            if arr[i] == target:
                continue
            res += (abs(target - arr[i]) // x)
        return res

Editorial

Approach 1: Sorting and Median

class Solution:
    def minOperations(self, grid, x):
        # Create a list to store all the numbers from the grid
        nums_array = []
        result = 0

        # Flatten the grid into nums_array
        for row in grid:
            for num in row:
                nums_array.append(num)

        # Sort nums_array in non-decreasing order to easily find the median
        nums_array.sort()

        length = len(nums_array)
        # Store the median element as the final common value
        final_common_number = nums_array[length // 2]

        # Iterate through each number in nums_array
        for number in nums_array:
            # If the remainder when divided by x is different, return -1
            if number % x != final_common_number % x:
                return -1
            # Add the number of operations required to make the current number equal to final_common_number
            result += abs(final_common_number - number) // x

        return result

Approach 2: Prefix and Suffix Sums

class Solution:
    def minOperations(self, grid, x):
        # Initialize an empty array to store all numbers
        nums_array = []
        result = float("inf")

        # Flatten the grid into nums_array and check if all elements have the same remainder when divided by x
        for row in range(len(grid)):
            for col in range(len(grid[0])):
                # If remainder of any element doesn't match the first element, return -1
                if grid[row][col] % x != grid[0][0] % x:
                    return -1
                nums_array.append(grid[row][col])

        # Sort nums_array in non-decreasing order to easily calculate operations
        nums_array.sort()

        length = len(nums_array)
        prefix_sum = [0] * length
        suffix_sum = [0] * length

        # Calculate the prefix sum up to each index (excluding the current element)
        for index in range(1, length):
            prefix_sum[index] = prefix_sum[index - 1] + nums_array[index - 1]

        # Calculate the suffix sum from each index (excluding the current element)
        for index in range(length - 2, -1, -1):
            suffix_sum[index] = suffix_sum[index + 1] + nums_array[index + 1]

        # Iterate through nums_array to calculate the number of operations for each potential common value
        for index in range(length):
            left_operations = (
                nums_array[index] * index - prefix_sum[index]
            ) // x
            right_operations = (
                suffix_sum[index] - nums_array[index] * (length - index - 1)
            ) // x
            # Update the result with the minimum operations needed
            result = min(result, left_operations + right_operations)

        return result

Approach 3: Two Pointers

class Solution:
    def minOperations(self, grid: list[list[int]], x: int) -> int:
        nums_array = []
        result = 0

        # Flatten the grid into nums_array and check remainder condition
        for row in range(len(grid)):
            for col in range(len(grid[0])):
                # If any element has a different remainder than the first element,
                # it is impossible to make all elements equal, so
                # return -1
                if grid[row][col] % x != grid[0][0] % x:
                    return -1
                nums_array.append(grid[row][col])

        nums_array.sort()

        length = len(nums_array)
        prefix_index = 0
        suffix_index = length - 1

        # Move prefix_index and suffix_index towards the middle
        while prefix_index < suffix_index:
            # If the prefix of equal elements is shorter than the suffix
            if prefix_index < length - suffix_index - 1:
                # Calculate the number of operations required to extend the prefix
                prefix_operations = (
                    (prefix_index + 1)
                    * (nums_array[prefix_index + 1] - nums_array[prefix_index])
                    // x
                )
                result += prefix_operations
                # Move the prefix index forward
                prefix_index += 1
            else:
                # Calculate the number of operations required to extend the suffix
                suffix_operations = (
                    (length - suffix_index)
                    * (nums_array[suffix_index] - nums_array[suffix_index - 1])
                    // x
                )
                result += suffix_operations
                # Move the suffix index backward
                suffix_index -= 1

        return result