Problem of The Day: Number of Ways to Split Array

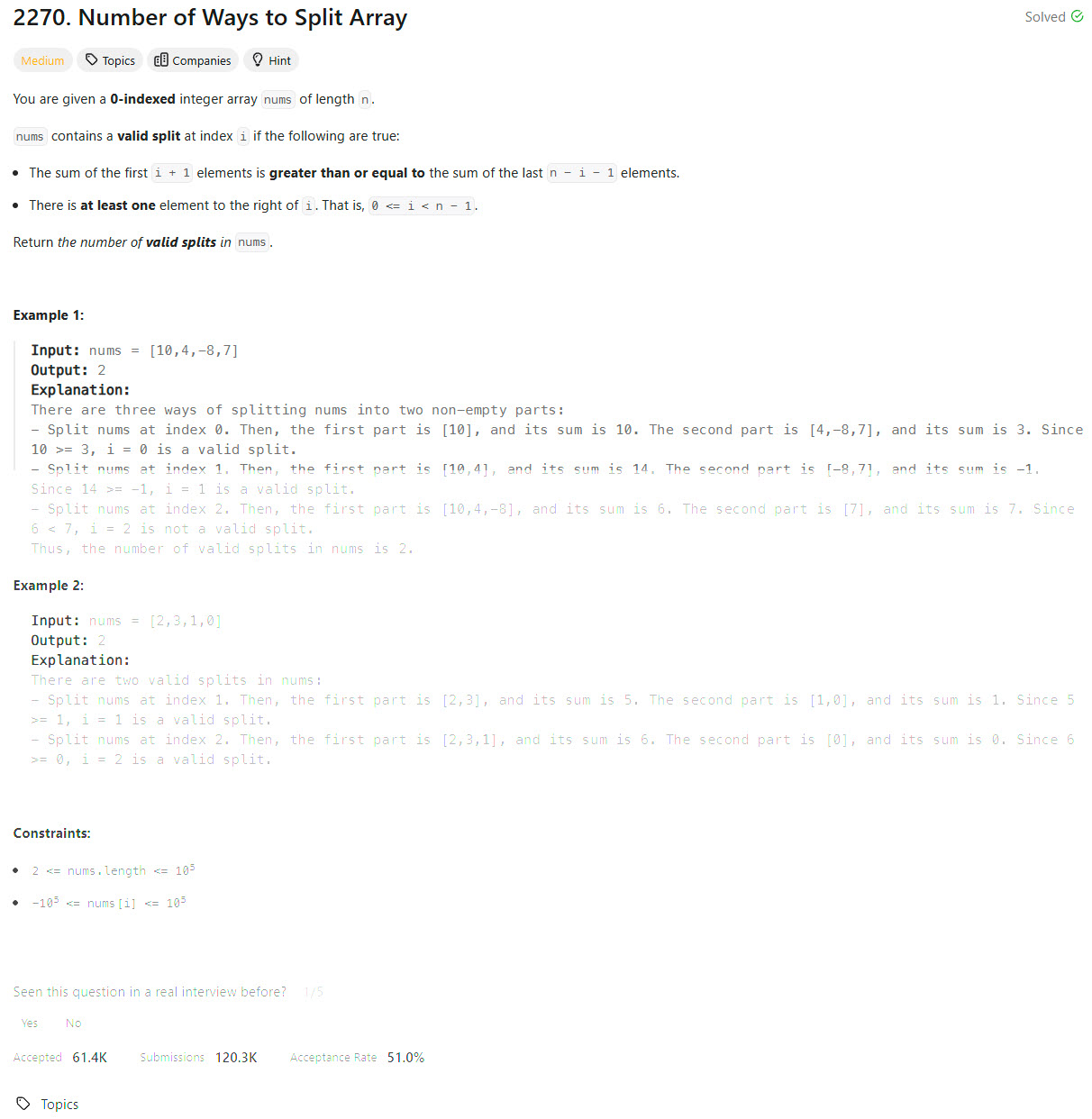
Problem Statement

Intuition

The problem involves finding a way to split an array such that the sum of the left subarray is greater than or equal to the sum of the right subarray. This can be solved by precomputing prefix and suffix sums for efficient comparisons.

Approach

1. Compute the prefix sum (L) for the array, where L[i] represents the sum of elements from the start of the array up to index i.
2. Compute the suffix sum (R) for the array, where R[i] represents the sum of elements from index i to the end of the array.
3. Iterate through the array up to the second-last element, and for each split at index i, compare L[i] and R[i+1]. Increment the result if L[i] >= R[i+1].

This approach ensures that we avoid recalculating sums repeatedly, making the solution efficient.

Complexity

• Time complexity:
  \(O(n)\)
  Computing prefix and suffix sums each take linear time, and iterating through the array for comparison is also linear.

• Space complexity:
  \(O(n)\)
  We use two additional arrays, L and R, each of size n to store prefix and suffix sums.

Code

class Solution:
    def waysToSplitArray(self, nums: List[int]) -> int:
        N = len(nums)
        L = [0] * N
        R = [0] * N
        curr_sum = 0
        res = 0
        for i, num in enumerate(nums):
            curr_sum += num
            L[i] = curr_sum

        curr_sum = 0
        for i in range(N - 1, -1, -1):
            curr_sum += nums[i]
            R[i] = curr_sum

        for i in range(N - 1):
            if L[i] >= R[i + 1]:
                res += 1
        return res

Editorial

Approach 1: Prefix Sum Array

class Solution:
    def waysToSplitArray(self, nums: list[int]) -> int:
        n = len(nums)
        # Prefix sum array to store cumulative sums
        pref_sum = [0] * n
        pref_sum[0] = nums[0]

        # Build prefix sum array
        for i in range(1, n):
            pref_sum[i] = pref_sum[i - 1] + nums[i]

        # Check each possible split position
        count = sum(
            1 for i in range(n - 1) if pref_sum[i] >= pref_sum[-1] - pref_sum[i]
        )

        return count

Approach 2: Optimized Prefix and Suffix Sums

class Solution:
    def waysToSplitArray(self, nums: list[int]) -> int:
        # Keep track of sum of elements on left and right sides
        left_sum = right_sum = 0

        # Initially all elements are on right side
        right_sum = sum(nums)

        # Try each possible split position
        count = 0
        for i in range(len(nums) - 1):
            # Move current element from right to left side
            left_sum += nums[i]
            right_sum -= nums[i]

            # Check if this creates a valid split
            if left_sum >= right_sum:
                count += 1

        return count