Problem of The Day: Largest Combination With Bitwise AND Greater Than Zero

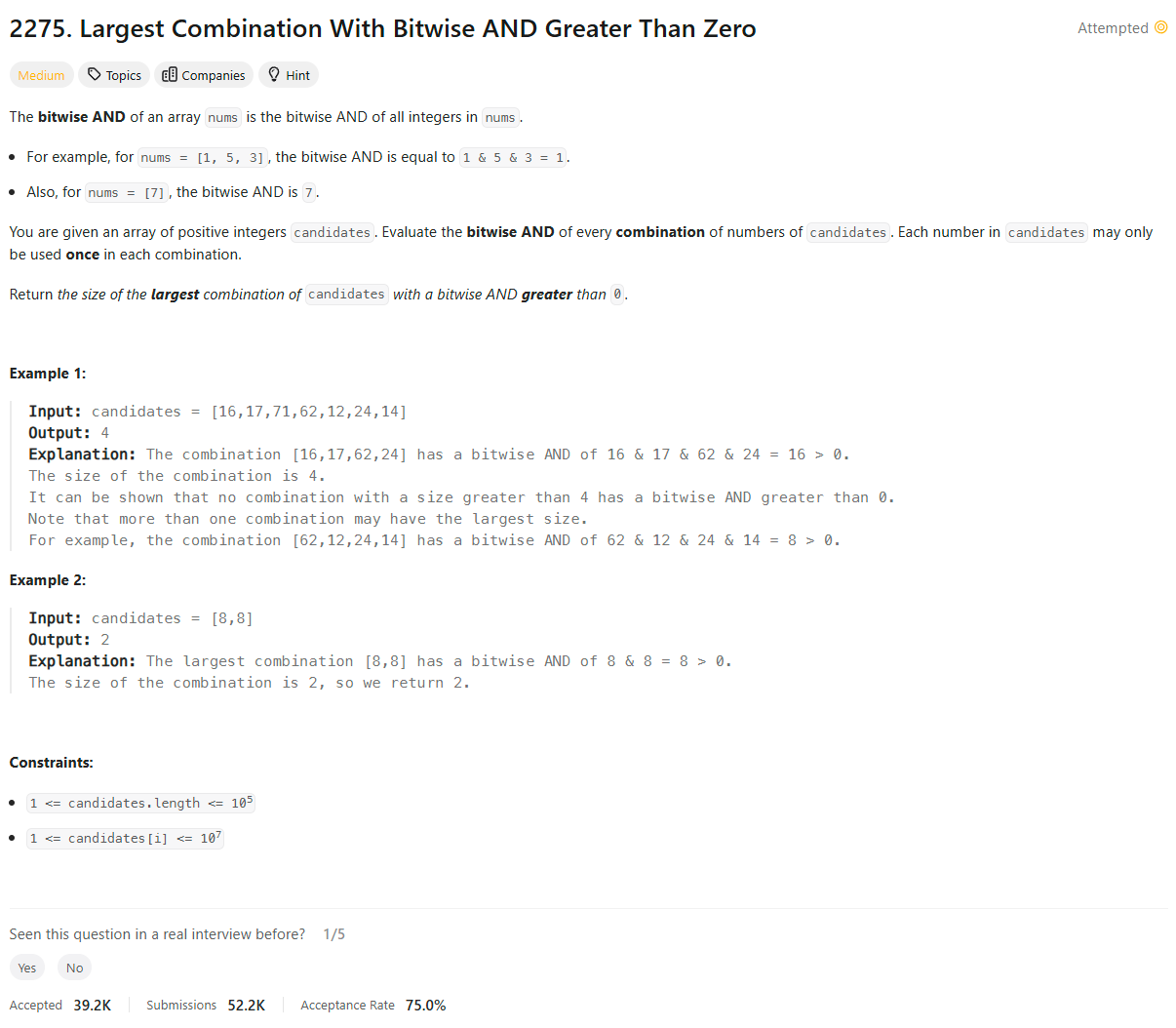
Problem Statement

Brute Force [TLE]

class Solution:
    def largestCombination(self, candidates: List[int]) -> int:
        res = float('-inf')
        N = len(candidates)
        for i in range(N):
            res = max(res, self.backtrack(i, candidates[i], candidates, len(candidates), 1))
        return res

    def backtrack(self, i, curr_bitwise, cand, n, size):
        if i == n:
            return size
        ans = size
        for j in range(i + 1, n):
            if curr_bitwise & cand[j] > 0:
                ans = max(ans, self.backtrack(j, curr_bitwise & cand[j], cand, n, size + 1))
        return ans

Editorial

Approach 1: Using a Bit Count Array

class Solution:
    def largestCombination(self, candidates: List[int]) -> int:
        # Initialize a list to store the count of each bit position.
        bit_count = [0] * 24
        for i in range(24):
            for num in candidates:
                # Check if the i-th bit is set.
                if (num & (1 << i)) != 0:
                    bit_count[i] += 1

        return max(bit_count)

• time: O(n)
• space: O(1)

Approach 2: Direct Maximum Bit Count

class Solution:
    def largestCombination(self, candidates):
        max_count = 0  # Variable to track the maximum count of set bits.
        for i in range(24):
            count = 0  # Count of numbers with the i-th bit set.
            for num in candidates:
                if (num & (1 << i)) != 0:  # Check if the i-th bit is set.
                    count += 1
            max_count = max(max_count, count)  # Update the maximum count.
        return max_count