Problem of The Day: Minimum Obstacle Removal to Reach Corner

Problem Statement

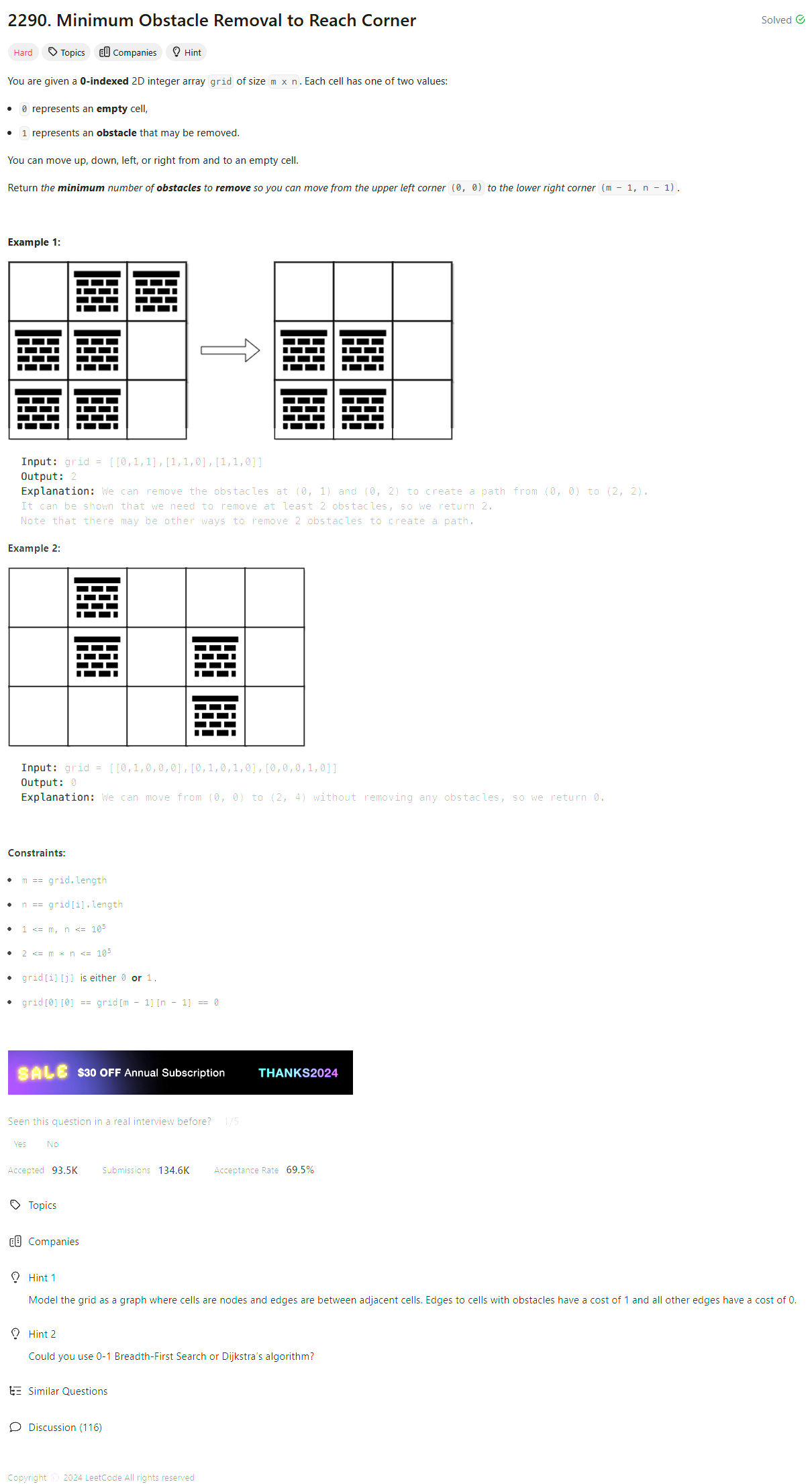
Notes:

• need to review Dijkstra and BFS 0-1 approach
• set to inf on empty cell

Dijkstra Algorithm Template

import heapq
from collections import defaultdict
from typing import List, Tuple, Dict

def dijkstra(n: int, edges: List[Tuple[int, int, int]], start: int) -> Dict[int, int]:
    """
    Implements Dijkstra's Algorithm to find the shortest path from a starting node.

    Parameters:
    - n: int -> Number of nodes in the graph.
    - edges: List[Tuple[int, int, int]] -> List of edges represented as (u, v, weight).
    - start: int -> Starting node for Dijkstra's algorithm.

    Returns:
    - distances: Dict[int, int] -> Dictionary where key is the node and value is the shortest distance from start.
    """
    # Build the graph as an adjacency list
    graph = defaultdict(list)
    for u, v, weight in edges:
        graph[u].append((v, weight))
        graph[v].append((u, weight))  # Uncomment this line if the graph is undirected.

    # Min-heap to prioritize nodes with smallest distance
    min_heap = [(0, start)]  # (distance, node)
    distances = {i: float('inf') for i in range(n)}  # Initialize distances to infinity
    distances[start] = 0  # Distance to the start node is 0

    while min_heap:
        curr_dist, curr_node = heapq.heappop(min_heap)

        # Skip if a better distance is already found
        if curr_dist > distances[curr_node]:
            continue

        # Relaxation step
        for neighbor, weight in graph[curr_node]:
            distance = curr_dist + weight
            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(min_heap, (distance, neighbor))

    return distances

# Example usage
if __name__ == "__main__":
    # Example input
    n = 5  # Number of nodes (0 to 4)
    edges = [
        (0, 1, 2),
        (0, 2, 4),
        (1, 2, 1),
        (1, 3, 7),
        (2, 4, 3),
        (3, 4, 1)
    ]
    start = 0
    shortest_distances = dijkstra(n, edges, start)
    print("Shortest distances from node", start, ":", shortest_distances)

Key Concepts

• Graph Representation: The graph is represented as an adjacency list for efficiency.
• Min-Heap: A priority queue is used to fetch the next node with the smallest tentative distance.
• Distance Relaxation: Update the shortest distance to a node when a better path is found.

Usage

1. Replace edges with your graph data.
2. Adjust the graph representation if the input uses a different format, e.g., adjacency matrix.
3. The return value distances contains the shortest distance from the start node to all other nodes.

Editorial Solution for this problem

Approach 1: Dijkstra’s Algorithm

class Solution:
    # Directions for movement: right, left, down, up
    directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]

    def minimumObstacles(self, grid):
        # Helper method to check if the cell is within the grid bounds
        def _is_valid(row, col):
            return 0 <= row < len(grid) and 0 <= col < len(grid[0])

        m, n = len(grid), len(grid[0])

        # Initialize distance matrix with infinity (large value)
        min_obstacles = [[float("inf")] * n for _ in range(m)]

        # Start from the top-left corner, accounting for its obstacle value
        min_obstacles[0][0] = grid[0][0]

        pq = [(min_obstacles[0][0], 0, 0)]  # (obstacles, row, col)

        while pq:
            obstacles, row, col = heapq.heappop(pq)

            # If we've reached the bottom-right corner, return the result
            if row == m - 1 and col == n - 1:
                return obstacles

            # Explore all four possible directions from the current cell
            for dr, dc in self.directions:
                new_row, new_col = row + dr, col + dc

                if _is_valid(new_row, new_col):
                    # Calculate the obstacles removed if moving to the new cell
                    new_obstacles = obstacles + grid[new_row][new_col]

                    # Update if we've found a path with fewer obstacles to the new cell
                    if new_obstacles < min_obstacles[new_row][new_col]:
                        min_obstacles[new_row][new_col] = new_obstacles
                        heapq.heappush(pq, (new_obstacles, new_row, new_col))

        return min_obstacles[m - 1][n - 1]

Approach 2: 0-1 Breadth-First Search (BFS)

class Solution:
    # Directions for movement: right, left, down, up
    _directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]

    def minimumObstacles(self, grid):
        # Helper method to check if the cell is within the grid bounds
        def _is_valid(row, col):
            return 0 <= row < len(grid) and 0 <= col < len(grid[0])

        m, n = len(grid), len(grid[0])

        # Distance matrix to store the minimum obstacles removed to reach each cell
        min_obstacles = [[float("inf")] * n for _ in range(m)]
        min_obstacles[0][0] = 0

        deque_cells = deque([(0, 0, 0)])  # (obstacles, row, col)

        while deque_cells:
            obstacles, row, col = deque_cells.popleft()

            # Explore all four possible directions from the current cell
            for dr, dc in self._directions:
                new_row, new_col = row + dr, col + dc

                if _is_valid(new_row, new_col) and min_obstacles[new_row][
                    new_col
                ] == float("inf"):
                    if grid[new_row][new_col] == 1:
                        # If it's an obstacle, add 1 to obstacles and push to the back
                        min_obstacles[new_row][new_col] = obstacles + 1
                        deque_cells.append((obstacles + 1, new_row, new_col))
                    else:
                        # If it's an empty cell, keep the obstacle count and push to the front
                        min_obstacles[new_row][new_col] = obstacles
                        deque_cells.appendleft((obstacles, new_row, new_col))

        return min_obstacles[m - 1][n - 1]