Problem of The Day: Max Sum of a Pair With Equal Sum of Digits

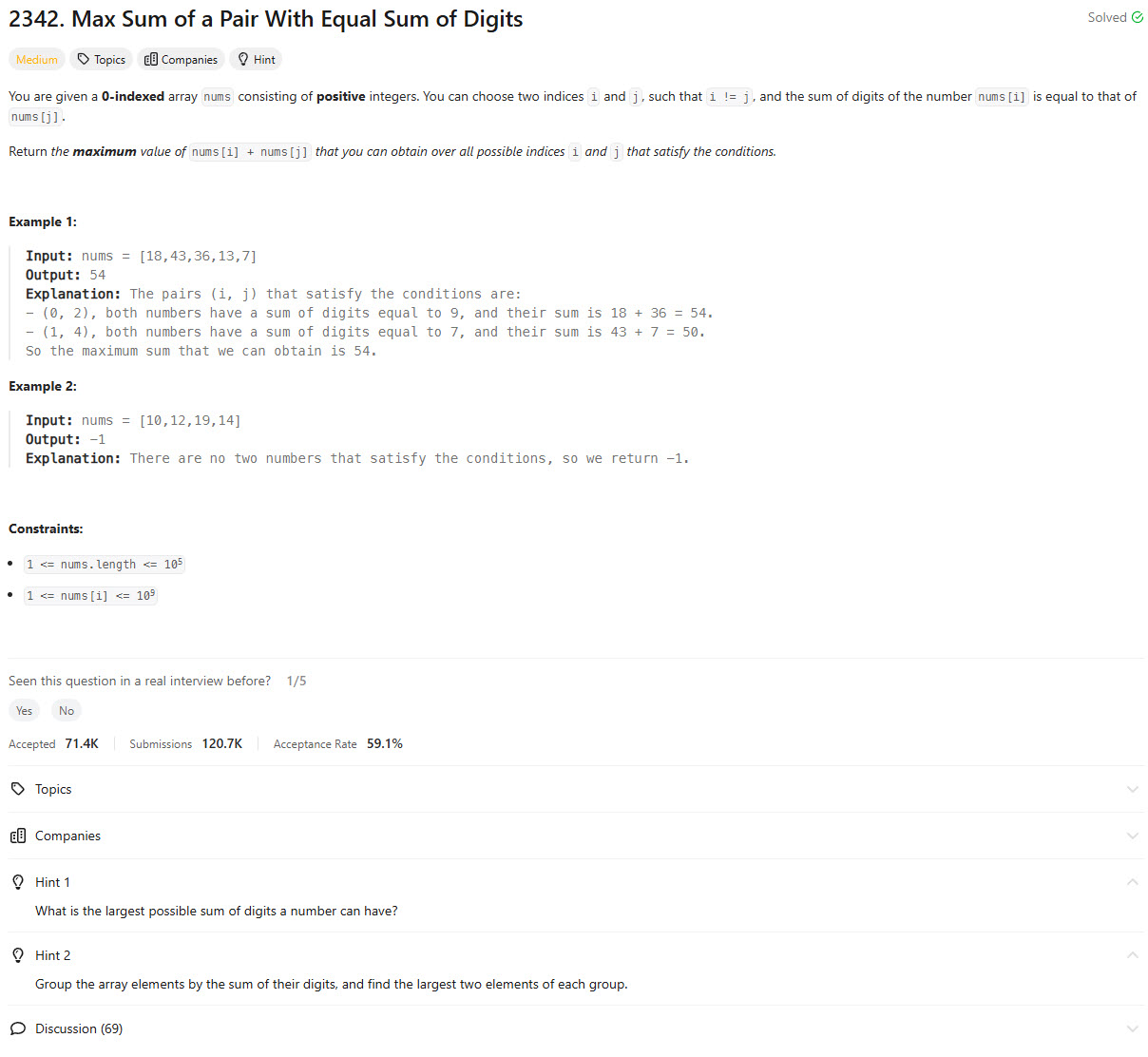
Problem Statement

Brute Force [TLE]

class Solution:
    def maximumSum(self, nums: List[int]) -> int:
        hash_map = defaultdict(list)
        res = -1

        def get_sum_digits(number):
            ans = 0
            while number > 0:
                ans += (number % 10)
                number //= 10
            return ans

        for num in nums:
            sum_digits = get_sum_digits(num)
            hash_map[sum_digits].append(num)

        for _, numbers in hash_map.items():
            if len(numbers) >= 2:
                n = len(numbers)
                for i in range(n - 1):
                    for j in range(i + 1, n):
                        res = max(res, numbers[i] + numbers[j])

        return res

Improved Algorithm using SortedList

class Solution:
    from sortedcontainers import SortedList
    def maximumSum(self, nums: List[int]) -> int:
        hash_map = defaultdict(SortedList)
        res = -1

        def get_sum_digits(number):
            ans = 0
            while number > 0:
                ans += (number % 10)
                number //= 10
            return ans

        for num in nums:
            sum_digits = get_sum_digits(num)
            hash_map[sum_digits].add(num)

        for _, numbers in hash_map.items():
            if len(numbers) >= 2:
                res = max(res, numbers[-1] + numbers[-2])
        return res

• time: O(n log n)
• space: O(n)

Editorial

Approach 1: Sorting

class Solution:
    # Helper function to compute the sum of digits of a number
    def calculate_digit_sum(self, num):
        digit_sum = 0
        while num > 0:
            digit_sum += num % 10
            num //= 10
        return digit_sum

    def maximumSum(self, nums):
        digit_sum_pairs = []

        # Store numbers with their digit sums as pairs
        for number in nums:
            digit_sum = self.calculate_digit_sum(number)
            digit_sum_pairs.append((digit_sum, number))

        # Sort based on digit sums, and if equal, by number value
        digit_sum_pairs.sort()

        max_pair_sum = -1

        # Iterate through the sorted array to find the maximum sum of pairs
        for index in range(1, len(digit_sum_pairs)):
            current_digit_sum = digit_sum_pairs[index][0]
            previous_digit_sum = digit_sum_pairs[index - 1][0]

            # If two consecutive numbers have the same digit sum
            if current_digit_sum == previous_digit_sum:
                current_sum = (
                    digit_sum_pairs[index][1] + digit_sum_pairs[index - 1][1]
                )
                max_pair_sum = max(max_pair_sum, current_sum)

        return max_pair_sum

• time: O(n log n)
• space: O(n)

Approach 2: Priority Queue

class Solution:
    # Helper function to compute the sum of digits of a number
    def calculate_digit_sum(self, num):
        digit_sum = 0
        while num > 0:
            digit_sum += num % 10
            num //= 10
        return digit_sum

    def maximumSum(self, nums):
        # List to store a heap for each possible digit sum (0 to 81)
        digit_sum_groups = [[] for _ in range(82)]

        max_pair_sum = -1

        # Group numbers by their digit sums, maintaining heap size of 2
        for number in nums:
            digit_sum = self.calculate_digit_sum(number)
            heapq.heappush(digit_sum_groups[digit_sum], number)

            # Keep only the top 2 largest numbers in the heap
            if len(digit_sum_groups[digit_sum]) > 2:
                heapq.heappop(
                    digit_sum_groups[digit_sum]
                )  # Remove the smallest element

        # Traverse the list to find the maximum pair sum for each group
        for min_heap in digit_sum_groups:
            if len(min_heap) == 2:
                first = heapq.heappop(min_heap)
                second = heapq.heappop(min_heap)
                max_pair_sum = max(max_pair_sum, first + second)

        return max_pair_sum

• time: O(n log n)
• space: O(log m)