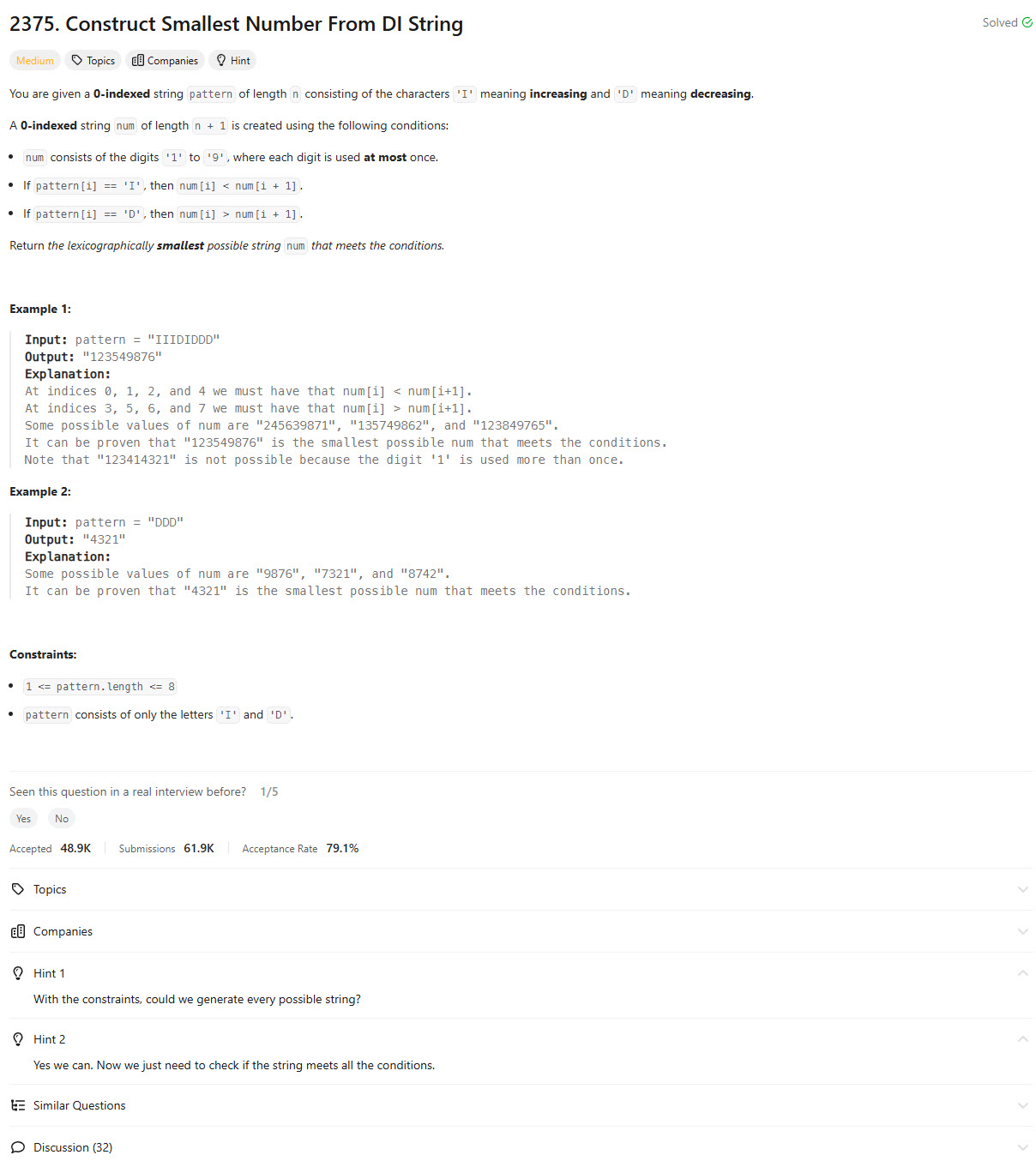
Problem Statement
Brute Force [TLE]
class Solution:
def smallestNumber(self, pattern: str) -> str:
all_strings = []
n = len(pattern) + 1
initial_string = ''.join(str(i) for i in range(1, n + 1))
_seq = set()
_used = [False] * len(initial_string)
def dfs(init_str, curr, used, seq):
if len(curr) == n:
seq.add(curr)
for i, c in enumerate(init_str):
if not used[i]:
used[i] = True
dfs(init_str, curr + c, used, seq)
used[i] = False
def filter_string(seq):
arr = sorted(list(seq))
for item in arr:
found = True
for i in range(len(pattern)):
if pattern[i] == 'I' and item[i] > item[i + 1]:
found = False
break
if pattern[i] == 'D' and item[i] < item[i + 1]:
found = False
break
if found:
return item
dfs(initial_string, "", _used, _seq)
return filter_string(_seq)
Greed Approach
class Solution:
def smallestNumber(self, pattern: str) -> str:
result = []
stack = []
num = 1
# Iterate through positions of pattern + one extra iteration for the last number
for i in range(len(pattern) + 1):
stack.append(str(num))
num += 1
# If at the end or the current pattern character is 'I', empty the stack into result.
if i == len(pattern) or pattern[i] == 'I':
while stack:
result.append(stack.pop())
return "".join(result)
Editorial
Approach 1: Brute Force
class Solution:
# Check if the current sequence matches the pattern of 'I' and 'D'
def check(self, number_sequence: str, pattern: str) -> bool:
for index in range(len(pattern)):
# Ensure the sequence is in increasing order at 'I' positions
if (
pattern[index] == "I"
and number_sequence[index] > number_sequence[index + 1]
):
return False
# Ensure the sequence is in decreasing order at 'D' positions
elif (
pattern[index] == "D"
and number_sequence[index] < number_sequence[index + 1]
):
return False
return True
def smallestNumber(self, pattern: str) -> str:
pattern_length = len(pattern)
# Generate sequence "123...n+1"
number_sequence = "".join(
str(num) for num in range(1, pattern_length + 2)
)
# Use permutations generator
for permutation in permutations(number_sequence):
permutation_str = "".join(permutation)
if self.check(permutation_str, pattern):
return permutation_str
return ""
Approach 2: Optimization with Bit Masking
class Solution:
def smallestNumber(self, pattern: str) -> str:
return str(self.find_smallest_number(pattern, 0, 0, 0))
# Recursively find the smallest number that satisfies the pattern
def find_smallest_number(
self,
pattern: str,
current_position: int,
used_digits_mask: int,
current_num: int,
) -> int:
# Base case: return the current number when the whole pattern is processed
if current_position > len(pattern):
return current_num
result = float("inf")
last_digit = current_num % 10
should_increment = (
current_position == 0 or pattern[current_position - 1] == "I"
)
# Try all possible digits (1 to 9) that are not yet used and follow the pattern
for current_digit in range(1, 10):
if (used_digits_mask & (1 << current_digit)) == 0 and (
current_digit > last_digit
) == should_increment:
result = min(
result,
self.find_smallest_number(
pattern,
current_position + 1,
used_digits_mask | (1 << current_digit),
current_num * 10 + current_digit,
),
)
return result
Approach 3: Regulated Brute Force via Recursion
class Solution:
def smallestNumber(self, pattern: str) -> str:
self.result = []
# Start building the sequence by calling the helper function
self.build_sequence(0, 0, pattern)
# Reverse the final result
return "".join(self.result[::-1])
# Recursively build the sequence
def build_sequence(
self, current_index: int, current_count: int, pattern: str
) -> int:
if current_index != len(pattern):
if pattern[current_index] == "I":
# If 'I', increment the count and move to the next index
self.build_sequence(
current_index + 1, current_index + 1, pattern
)
else:
# If 'D', keep the count and move to the next index
current_count = self.build_sequence(
current_index + 1, current_count, pattern
)
self.result.append(str(current_count + 1))
# Return the next count for the sequence
return current_count + 1
Approach 4: Using Stack
class Solution:
def smallestNumber(self, pattern: str) -> str:
result = []
num_stack = []
# Iterate through the pattern
for index in range(len(pattern) + 1):
# Push the next number onto the stack
num_stack.append(index + 1)
# If 'I' is encountered or we reach the end, pop all stack elements
if index == len(pattern) or pattern[index] == "I":
while num_stack:
result.append(str(num_stack.pop()))
return "".join(result)
Approach 5: Greedy Approach with Sliding Window Reversal
class Solution:
def smallestNumber(self, pattern: str) -> str:
result = []
# Iterate through the pattern and build the result
previous_index = 0
for current_index in range(len(pattern) + 1):
result.append(str(1 + current_index))
# Reverse the substring starting from previous_index when necessary
if current_index == len(pattern) or pattern[current_index] == "I":
result[previous_index:] = reversed(result[previous_index:])
previous_index = current_index + 1
return "".join(result)
Approach 6: Optimized Greedy Approach with Precomputed ‘D’ Segments
class Solution:
def smallestNumber(self, pattern: str) -> str:
pattern_length = len(pattern)
max_so_far = curr_max = temp = 0
# List to store lengths of decreasing subsequences in the pattern
arr_D = [0 for _ in range(pattern_length + 2)]
# Compute the lengths of decreasing subsequences in the pattern
for pattern_index in range(pattern_length, -1, -1):
if pattern_index < pattern_length and pattern[pattern_index] == "D":
# If 'D', increment the length of the decreasing sequence
arr_D[pattern_index] = arr_D[pattern_index + 1] + 1
result = ""
# Build the result string based on the pattern
for position in range(pattern_length + 1):
if position < pattern_length and pattern[position] == "I":
# If 'I', assign the next maximum digit and append it to the
# result
max_so_far += 1
result += str(max_so_far)
# Update the max digit encountered so far
max_so_far = max(max_so_far, curr_max)
# Reset current max for the next iteration
curr_max = 0
else:
# If 'D', calculate the appropriate digit and append it to the
# result
temp = 1 + max_so_far + arr_D[position]
result += str(temp)
# Update the current max value
curr_max = max(curr_max, temp)
return result
