Problem of The Day: Maximum Sum of Distinct Subarrays With Length K

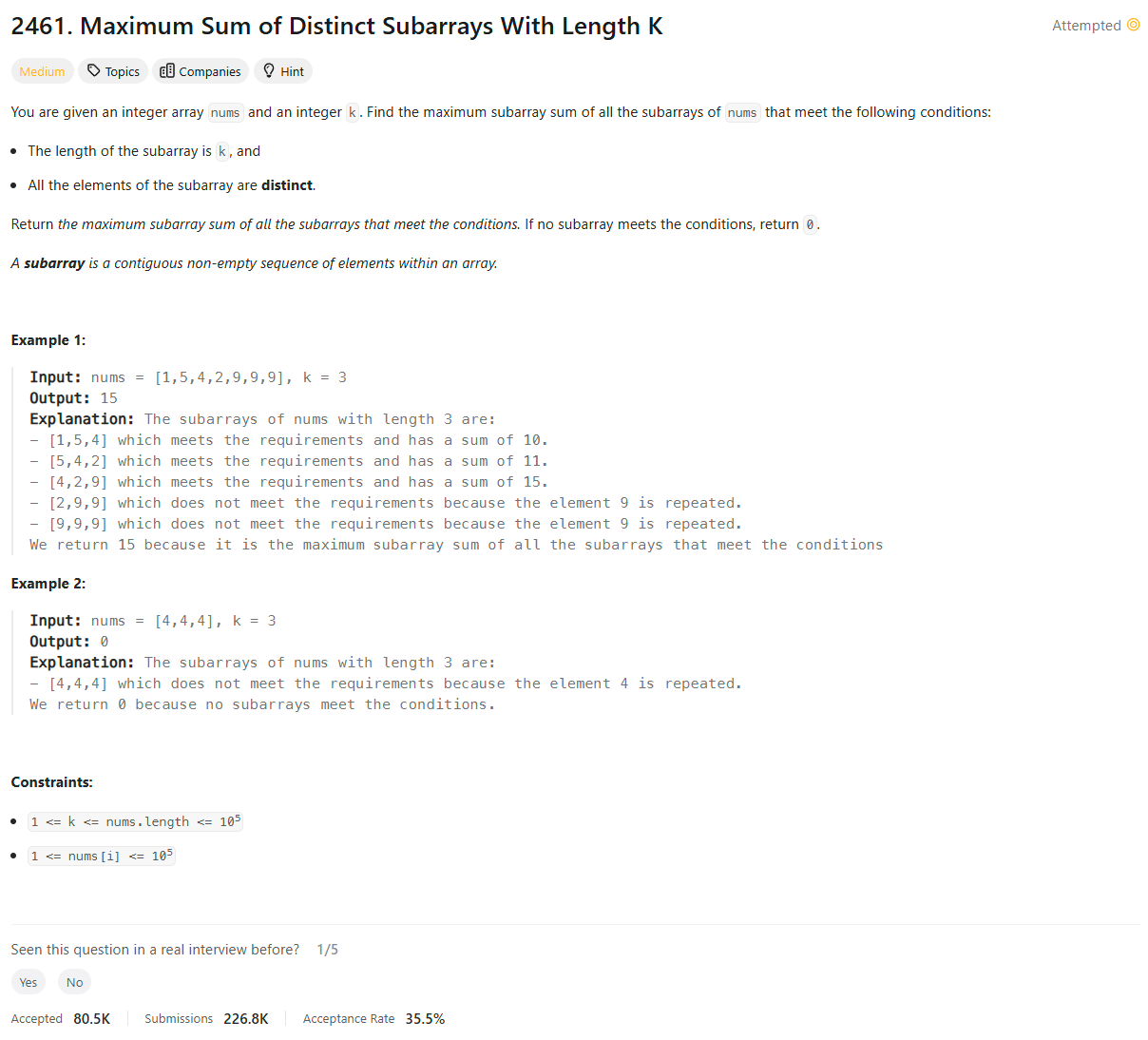
Problem Statement

Brute Force [TLE]

class Solution:
    def maximumSubarraySum(self, nums: List[int], k: int) -> int:
        start, end = 0, k - 1
        N = len(nums)
        res = 0
        arr = deque()
        curr_sum = 0
        for i in range(k):
            arr.append(nums[i])
            curr_sum += nums[i]

        for end in range(k, N):
            if len(set(arr)) == k:
                res = max(res, curr_sum)
            curr_sum -= nums[start]
            start += 1
            arr.popleft()
            arr.append(nums[end])
            curr_sum += nums[end]

        if len(set(arr)) == k:
            res = max(res, curr_sum)
        return res

Intuition

The goal is to find the maximum sum of a subarray of size k in a given list, ensuring that all elements in the subarray are unique. To achieve this, a sliding window approach can efficiently track subarray sums and uniqueness constraints.

Approach

1. Sliding Window Technique:
   Use two pointers (start and end) to maintain a window of size at most k. Adjust the window dynamically based on conditions:

   • If a duplicate element is found within the window, move the start pointer to exclude the earlier occurrence of the duplicate, updating the current sum and hash map accordingly.
   • If the window size equals k, compute the maximum sum and shrink the window by moving the start pointer forward.

2. Tracking Uniqueness:
   A hash map (hash_map) is used to store the most recent index of each element in the current window. This helps quickly identify and handle duplicates.

3. Maintaining the Current Sum:
   A variable (curr_sum) tracks the sum of the current window. When the window changes (e.g., due to duplicates or exceeding size k), the sum is adjusted by subtracting the values of excluded elements.

4. Result Calculation:
   Continuously update the result (res) with the maximum sum encountered when the window size equals k.

Complexity

• Time Complexity:
  \(O(n)\)
  Each element is processed at most twice (once when entering the window and once when exiting).

• Space Complexity:
  \(O(k)\)
  The hash map and the sliding window can hold up to k elements.

Code

class Solution:
    def maximumSubarraySum(self, nums: List[int], k: int) -> int:
        start, end = 0, k - 1
        N = len(nums)
        res = 0
        curr_sum = 0
        hash_map = defaultdict(int)

        for end in range(N):
            # Handle duplicates
            if nums[end] in hash_map:
                index = hash_map[nums[end]]
                for i in range(start, index + 1):
                    curr_sum -= nums[i]
                    if nums[i] in hash_map:
                        del hash_map[nums[i]]
                start = index + 1

            # Update current window
            hash_map[nums[end]] = end
            curr_sum += nums[end]

            # Check if window size equals k
            if end - start + 1 == k:
                res = max(res, curr_sum)
                curr_sum -= nums[start]
                if nums[start] in hash_map:
                    del hash_map[nums[start]]
                start += 1

        return res

Editorial

Approach: Sliding Window

class Solution:
    def maximumSubarraySum(self, nums: List[int], k: int) -> int:
        ans = 0
        current_sum = 0
        begin = 0
        end = 0
        num_to_index = {}

        while end < len(nums):
            curr_num = nums[end]
            last_occurrence = num_to_index.get(curr_num, -1)
            # if current window already has number or if window is too big, adjust window
            while begin <= last_occurrence or end - begin + 1 > k:
                current_sum -= nums[begin]
                begin += 1
            num_to_index[curr_num] = end
            current_sum += nums[end]
            if end - begin + 1 == k:
                ans = max(ans, current_sum)
            end += 1
        return ans

• time: O(N)
• space: O(N)