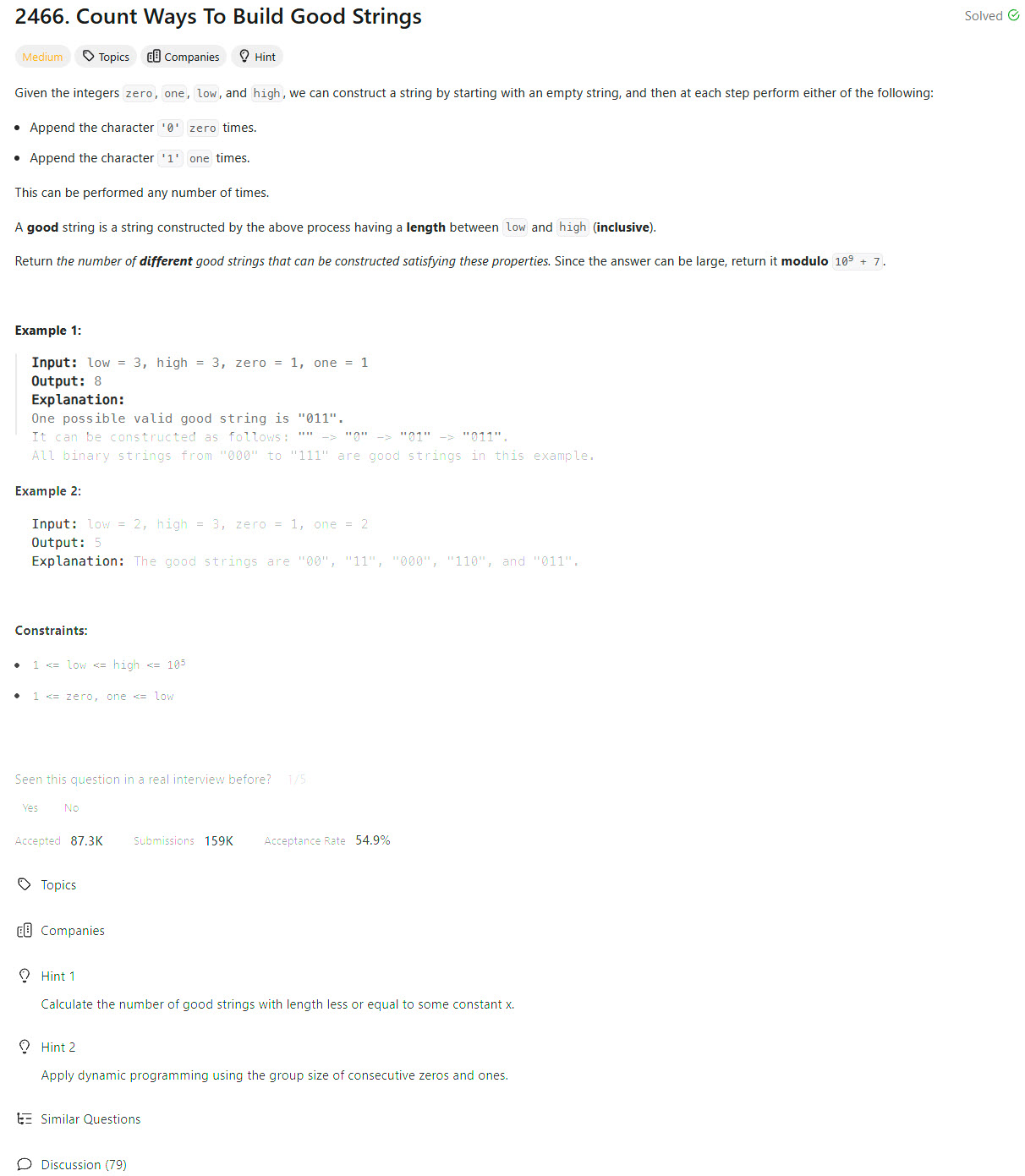
Problem Statement
Brute Force [TLE]
class Solution:
def countGoodStrings(self, low: int, high: int, zero: int, one: int) -> int:
MOD = 10**9 + 7
self.count = 0
def dfs(length, count):
if length > high:
return
if low <= length <= high:
self.count = (self.count + 1) % MOD
dfs(length + zero, count)
dfs(length + one, count)
dfs(0, 0)
return self.count
Memoization Approach [MLE]
class Solution:
def countGoodStrings(self, low: int, high: int, zero: int, one: int) -> int:
MOD = 10**9 + 7
self.count = 0
def dfs(length, zero_count, one_count, count):
if length > high:
return count % MOD
if (length, zero_count, one_count) in memo:
return memo[(length, zero_count, one_count)]
if low <= length <= high:
count = (count + 1) % MOD
zero_path = dfs(length + zero, zero_count + 1, one_count, count)
one_path = dfs(length + one, zero_count, one_count + 1, count)
memo[(length, zero_count, one_count)] = zero_path + one_path
return zero_path + one_path
memo = defaultdict(int)
return dfs(0, 0, 0, 0) // 2 % MOD
Improved Approach
class Solution:
def countGoodStrings(self, low: int, high: int, zero: int, one: int) -> int:
MOD = 10**9 + 7
# Memoization dictionary to cache results
memo = {}
def dfs(length):
# If length exceeds `high`, return 0 (invalid case)
if length > high:
return 0
# If the result for the current length is already computed, return it
if length in memo:
return memo[length]
# Count this string if it's within the valid range [low, high]
count = 1 if low <= length <= high else 0
# Recursively add valid strings by appending `zero` or `one`
count += dfs(length + zero)
count += dfs(length + one)
# Cache the result modulo MOD and return
memo[length] = count % MOD
return memo[length]
# Start DFS from length 0
return dfs(0)
Editorial
Approach 1: Dynamic Programming (Iterative).
class Solution:
def countGoodStrings(self, low: int, high: int, zero: int, one: int) -> int:
# Use dp[i] to record to number of good strings of length i.
dp = [1] + [0] * (high)
mod = 10 ** 9 + 7
# Iterate over each length `end`.
for end in range(1, high + 1):
# check if the current string can be made by append zero `0`s or one `1`s.
if end >= zero:
dp[end] += dp[end - zero]
if end >= one:
dp[end] += dp[end - one]
dp[end] %= mod
# Add up the number of strings with each valid length [low ~ high].
return sum(dp[low : high + 1]) % mod
Approach 2: Dynamic Programming (Recursive)
class Solution:
def countGoodStrings(self, low: int, high: int, zero: int, one: int) -> int:
# Use dp[i] to record to number of good strings of length i.
dp = [1] + [-1] * (high)
mod = 10 ** 9 + 7
# Find the number of good strings of length `end`.
def dfs(end):
if dp[end] != -1:
return dp[end]
count = 0
if end >= zero:
count += dfs(end - zero)
if end >= one:
count += dfs(end - one)
dp[end] = count % mod
return dp[end]
# Add up the number of strings with each valid length [low ~ high].
return sum(dfs(end) for end in range(low, high + 1)) % mod
