Problem of The Day: Minimum Number of Operations to Sort a Binary Tree by Level
Problem Statement
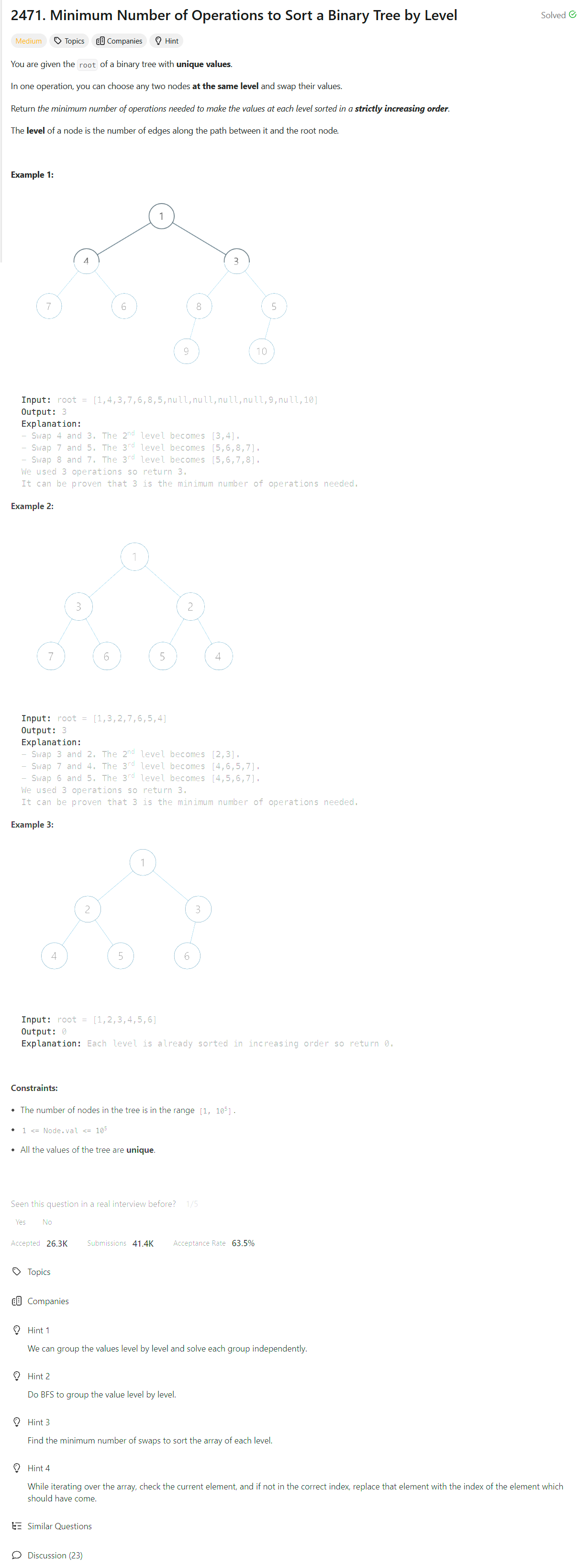
Intuition
The problem involves determining the minimum number of operations required to transform a binary tree’s node values at each level into sorted order. The main intuition is that sorting each level can be treated as a permutation problem, where we need to count the number of swaps required to transform an array into its sorted order.
Approach
-
Level Order Traversal:
- Use a queue to perform a level order traversal of the binary tree. This allows us to process each level independently.
- For each level, collect the node values in an array.
-
Sorting and Swapping:
- Sort the collected array for the current level.
- Use a greedy approach to count the minimum swaps needed to rearrange the original array into the sorted order.
- For each mismatch between the current and sorted array, swap the values to their correct positions, updating the count of operations.
-
Repeat for All Levels:
- Continue this process for all levels of the tree, accumulating the total count of swaps.
-
Result:
- The final count represents the minimum number of operations required to sort the binary tree levels.
Complexity
-
Time complexity:
- Level order traversal: \(O(n)\), where \(n\) is the number of nodes in the binary tree.
- Sorting each level: \(O(k \log k)\) per level, where \(k\) is the number of nodes at that level.
- Swapping: \(O(k)\) per level for finding and swapping elements.
- In the worst case (complete binary tree), the total complexity is approximately \(O(n \log n)\).
-
Space complexity:
- Queue for level order traversal: \(O(w)\), where \(w\) is the maximum width of the tree (at most \(n/2\) for a complete binary tree).
- Array to store level values: \(O(w)\).
- Total space complexity: \(O(w)\).
Code
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minimumOperations(self, root: Optional[TreeNode]) -> int:
from collections import deque
queue = deque()
queue.append(root)
res = 0
while queue:
n = len(queue)
arr = []
for i in range(n):
node = queue.popleft()
if node:
arr.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
sorted_arr = sorted(arr)
for i in range(len(arr)):
val = arr[i]
if val != sorted_arr[i]:
j = arr.index(sorted_arr[i])
arr[i], arr[j] = arr[j], arr[i]
res += 1
return res
Editorial
Approach 1: Hash Map
class Solution:
def minimumOperations(self, root: Optional["TreeNode"]) -> int:
queue = deque([root])
total_swaps = 0
# Process tree level by level using BFS
while queue:
level_size = len(queue)
level_values = []
# Store level values and add children to queue
for _ in range(level_size):
node = queue.popleft()
level_values.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
# Add minimum swaps needed for current level
total_swaps += self._get_min_swaps(level_values)
return total_swaps
# Calculate minimum swaps needed to sort an array
def _get_min_swaps(self, original: list) -> int:
swaps = 0
target = sorted(original)
# Map to track current positions of values
pos = {val: idx for idx, val in enumerate(original)}
# For each position, swap until correct value is placed
for i in range(len(original)):
if original[i] != target[i]:
swaps += 1
# Update position of swapped values
cur_pos = pos[target[i]]
pos[original[i]] = cur_pos
original[cur_pos] = original[i]
return swaps
Approach 2: Bit Manipulation
class Solution:
# Constants for bit manipulation
_SHIFT = 20
_MASK = 0xFFFFF
def minimumOperations(self, root: Optional["TreeNode"]) -> int:
queue = deque([root])
swaps = 0
# Process tree level by level using BFS
while queue:
level_size = len(queue)
nodes = []
# Store node values with encoded positions
for i in range(level_size):
node = queue.popleft()
# Encode value and index: high 20 bits = value, low 20 bits = index
nodes.append((node.val << self._SHIFT) + i)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
# Sort nodes by their values (high 20 bits)
nodes.sort()
# Count swaps needed to match indices with original positions
i = 0
while i < level_size:
orig_pos = nodes[i] & self._MASK
if orig_pos != i:
# Swap nodes and decrement i to recheck current position
nodes[i], nodes[orig_pos] = nodes[orig_pos], nodes[i]
swaps += 1
i -= 1
i += 1
return swaps