Thomas Ngo

Software Engineer

3 minute read

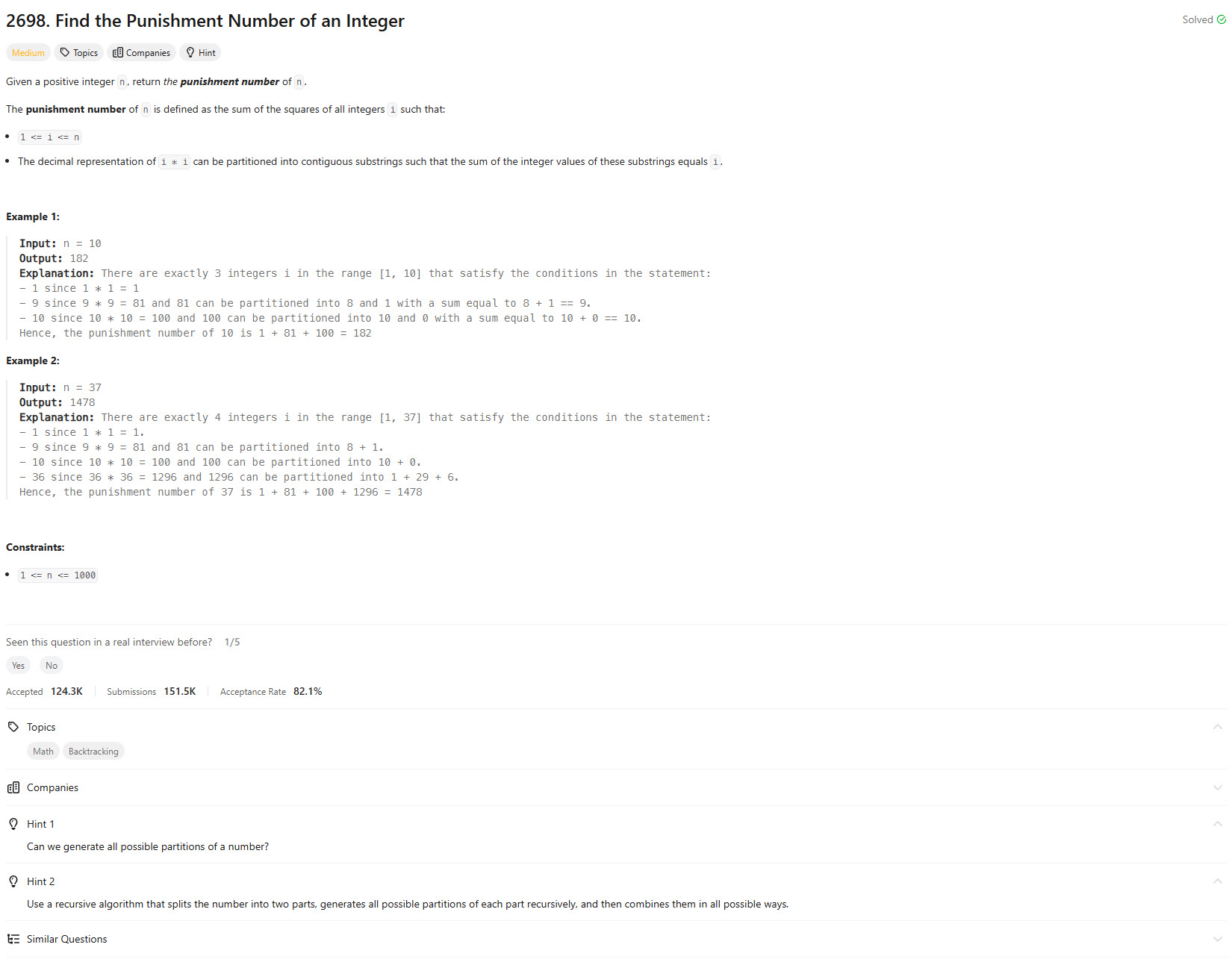
Problem Statement

problem

Intuition

The problem requires finding numbers whose squared value can be partitioned into segments that sum up to the original number. The core idea is to iterate through numbers, square them, and check if the square can be split into segments summing to the original number.

Approach

  1. Iterate Through Numbers: Loop through numbers from 1 to n, calculating their square value.
  2. Recursive Backtracking: Implement a helper function is_punishment_number to determine if the squared value can be partitioned into segments summing to the original number.
    • Convert the squared number into a string.
    • Try different partitions using recursion.
    • If a valid partition is found, return True.
  3. Summing Valid Squared Values: If a number satisfies the condition, add its square to the result.

Complexity

  • Time Complexity:
    • The backtracking approach tries different partitions, leading to an exponential time complexity in the worst case: \(O(2^m)\) where m is the number of digits in n^2.
  • Space Complexity:
    • The recursion depth is limited to the number of digits in n^2, so the space complexity is \(O(m)\).

Code

class Solution:
    def punishmentNumber(self, n: int) -> int:
        res = 0
        def is_punishment_number(start, num, target, curr):
            num_str = str(num)
            if start == len(num_str):
                return sum(curr) == target

            for i in range(start, len(num_str)):
                curr.append(int(num_str[start:i + 1]))
                if is_punishment_number(i + 1, num, target, curr):
                    return True
                curr.pop()
            return False

        for i in range(1, n + 1):
            square_val = i * i
            if is_punishment_number(0, square_val, i, []):
                res += square_val
        return res

Editorial

Approach 1: Memoization

class Solution:
    def find_partitions(
        self, start_index, current_sum, string_num, target, memo
    ):
        # Check if partition is valid
        if start_index == len(string_num):
            return current_sum == target

        # Invalid partition found, so we return False
        if current_sum > target:
            return False

        # If the result for this state is already calculated, return it
        if memo[start_index][current_sum] != -1:
            return memo[start_index][current_sum] == 1

        partition_found = False

        # Iterate through all possible substrings starting with start_index
        for current_index in range(start_index, len(string_num)):
            # Create partition
            current_string = string_num[start_index : current_index + 1]
            addend = int(current_string)

            # Recursively check if valid partition can be found
            partition_found = partition_found or self.find_partitions(
                current_index + 1,
                current_sum + addend,
                string_num,
                target,
                memo,
            )
            if partition_found:
                memo[start_index][current_sum] = 1
                return True

        # Memoize the result for future reference and return its result
        memo[start_index][current_sum] = 0
        return False

    def punishmentNumber(self, n: int) -> int:
        punishment_num = 0
        # Iterate through numbers in range [1, n]
        for current_num in range(1, n + 1):
            square_num = current_num * current_num
            string_num = str(square_num)

            # Initialize values in memoization array
            memo_array = [
                [-1] * (current_num + 1) for _ in range(len(string_num))
            ]

            # Check if valid partition can be found and add squared number if so
            if self.find_partitions(0, 0, string_num, current_num, memo_array):
                punishment_num += square_num

        return punishment_num

Approach 2: Recursion of Strings

class Solution:
    def can_partition(self, string_num, target):
        # Valid Partition Found
        if not string_num and target == 0:
            return True

        # Invalid Partition Found
        if target < 0:
            return False

        # Recursively check all partitions for a valid partition
        for index in range(len(string_num)):
            left = string_num[: index + 1]
            right = string_num[index + 1 :]
            left_num = int(left)

            if self.can_partition(right, target - left_num):
                return True

        return False

    def punishmentNumber(self, n: int) -> int:
        punishment_num = 0

        # Iterate through numbers in range [1, n]
        for current_num in range(1, n + 1):
            square_num = current_num * current_num

            # Check if valid partition can be found and add squared number if so
            if self.can_partition(str(square_num), current_num):
                punishment_num += square_num

        return punishment_num

Approach 3: Recursion of Integers

class Solution:
    def can_partition(self, num, target):
        # Invalid partition found
        if target < 0 or num < target:
            return False

        # Valid partition found
        if num == target:
            return True

        # Recursively check all partitions for a valid partition
        return (
            self.can_partition(num // 10, target - num % 10)
            or self.can_partition(num // 100, target - num % 100)
            or self.can_partition(num // 1000, target - num % 1000)
        )

    def punishmentNumber(self, n: int) -> int:
        punishment_num = 0

        # Iterate through numbers in range [1, n]
        for current_num in range(1, n + 1):
            square_num = current_num * current_num

            # Check if valid partition can be found and add squared number if so
            if self.can_partition(square_num, current_num):
                punishment_num += square_num

        return punishment_num

You may also enjoy