Problem of The Day: Continuous Subarrays

Problem Statement

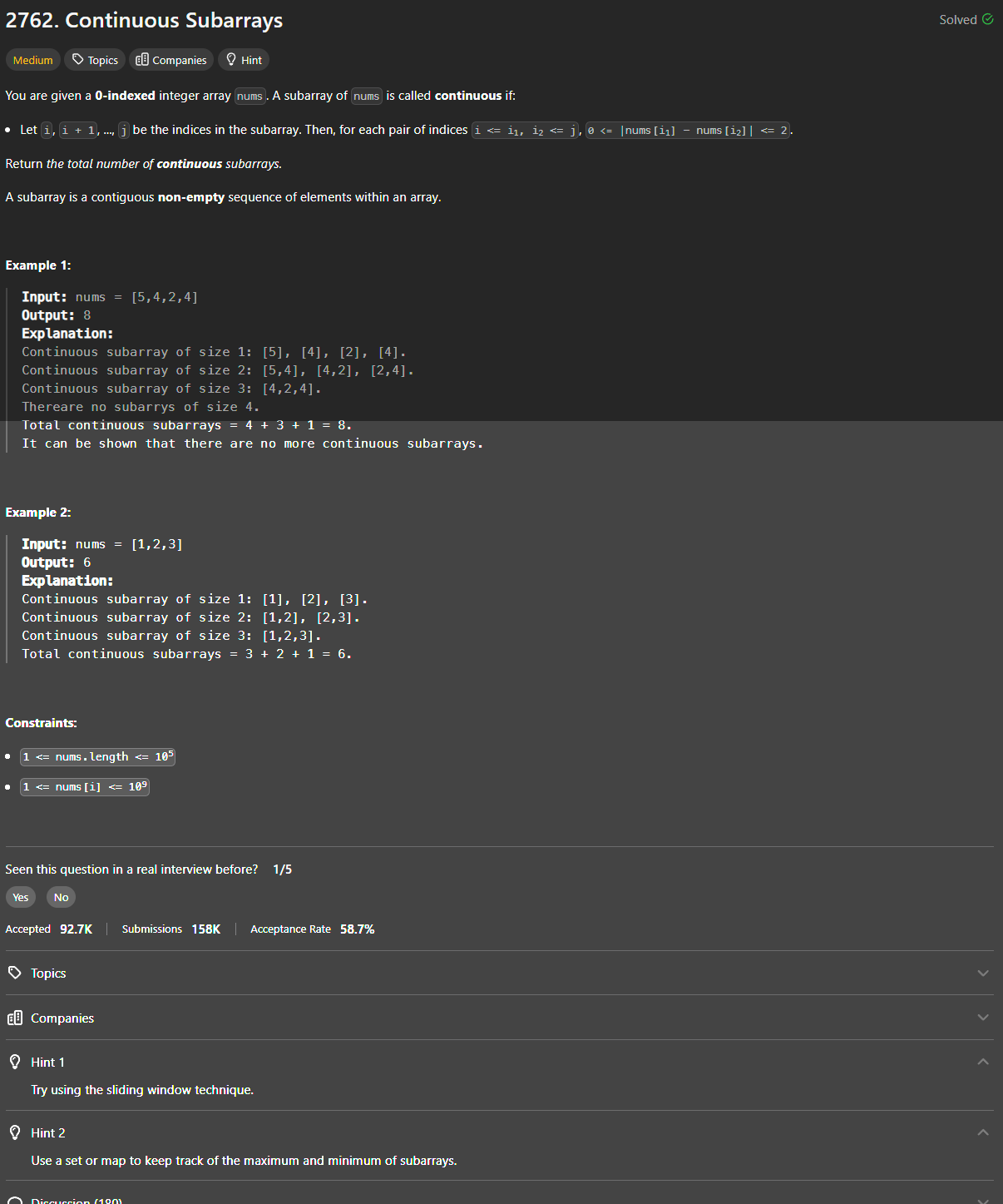
• Tips:
  • use two pointers / sliding windows
  • to calculate the subarrays use formula right_index - left_index + 1

Brute Force [TLE]

class Solution:
    def continuousSubarrays(self, nums: List[int]) -> int:
        window = 2
        N = len(nums)
        res = N

        def isValid(arr):
            for i in range(len(arr)):
                for j in range(len(arr)):
                    val = abs(arr[j] - arr[i])
                    if val < 0 or val > 2:
                        return False
            return 0 <= abs(arr[0] - arr[-1]) <= 2

        while window <= N:
            for i in range(N - window + 1):
                if isValid(nums[i:i + window]):
                    res += 1
            window += 1

        return res

class Solution:
    def continuousSubarrays(self, nums: List[int]) -> int:
        window = 2
        N = len(nums)
        res = N

        def isValid(arr):
            max_val = float('-inf')
            min_val = float('inf')
            for x in arr:
                max_val = max(max_val, x)
                min_val = min(min_val, x)

            return 0 <= max_val - min_val <= 2

        while window <= N:
            for i in range(N - window + 1):
                if isValid(nums[i:i + window]):
                    res += 1
            window += 1

        return res

Editorial

Approach 1: Sorted Map

class Solution:
    def continuousSubarrays(self, nums: List[int]) -> int:
        # Map to maintain sorted frequency map of current window
        freq = {}
        left = right = 0
        count = 0  # Total count of valid subarrays

        while right < len(nums):
            # Add current element to frequency map
            freq[nums[right]] = freq.get(nums[right], 0) + 1

            # While window violates the condition |nums[i] - nums[j]| ≤ 2
            # Shrink window from left
            while max(freq) - min(freq) > 2:
                # Remove leftmost element from frequency map
                freq[nums[left]] -= 1
                if freq[nums[left]] == 0:
                    del freq[nums[left]]
                left += 1

            # Add count of all valid subarrays ending at right
            count += right - left + 1
            right += 1

        return count

Approach 2: Priority Queue

class Solution:
    def continuousSubarrays(self, nums: List[int]) -> int:
        # Two heaps to track min/max indices, sorted by nums[index]
        min_heap = []  # (nums[i], i) tuples for min tracking
        max_heap = []  # (-nums[i], i) tuples for max tracking
        left = right = 0
        count = 0

        while right < len(nums):
            # Add current index to both heaps
            # For max heap, negate value to convert min heap to max heap
            heapq.heappush(min_heap, (nums[right], right))
            heapq.heappush(max_heap, (-nums[right], right))

            # While window violates |nums[i] - nums[j]| ≤ 2
            # Shrink window from left and remove outdated indices
            while left < right and -max_heap[0][0] - min_heap[0][0] > 2:
                left += 1

                # Remove indices outside window from both heaps
                while min_heap and min_heap[0][1] < left:
                    heapq.heappop(min_heap)
                while max_heap and max_heap[0][1] < left:
                    heapq.heappop(max_heap)

            count += right - left + 1
            right += 1

        return count

Approach 3: Monotonic Deque

class Solution:
    def continuousSubarrays(self, nums: List[int]) -> int:
        # Monotonic deque to track maximum and minimum elements
        max_q = deque()
        min_q = deque()
        left = 0
        count = 0

        for right, num in enumerate(nums):
            # Maintain decreasing monotonic deque for maximum values
            while max_q and nums[max_q[-1]] < num:
                max_q.pop()
            max_q.append(right)

            # Maintain increasing monotonic deque for minimum values
            while min_q and nums[min_q[-1]] > num:
                min_q.pop()
            min_q.append(right)

            # Shrink window if max-min difference exceeds 2
            while max_q and min_q and nums[max_q[0]] - nums[min_q[0]] > 2:
                # Move left pointer past the element that breaks the condition
                if max_q[0] < min_q[0]:
                    left = max_q[0] + 1
                    max_q.popleft()
                else:
                    left = min_q[0] + 1
                    min_q.popleft()

            # Add count of all valid subarrays ending at current right pointer
            count += right - left + 1

        return count

Approach 4: Optimized Two Pointer

class Solution:
    def continuousSubarrays(self, nums: List[int]) -> int:
        right = left = 0
        window_len = total = 0

        # Initialize window with first element
        cur_min = cur_max = nums[right]

        for right in range(len(nums)):
            # Update min and max for current window
            cur_min = min(cur_min, nums[right])
            cur_max = max(cur_max, nums[right])

            # If window condition breaks (diff > 2)
            if cur_max - cur_min > 2:
                # Add subarrays from previous valid window
                window_len = right - left
                total += window_len * (window_len + 1) // 2

                # Start new window at current position
                left = right
                cur_min = cur_max = nums[right]

                # Expand left boundary while maintaining condition
                while left > 0 and abs(nums[right] - nums[left - 1]) <= 2:
                    left -= 1
                    cur_min = min(cur_min, nums[left])
                    cur_max = max(cur_max, nums[left])

                # Remove overcounted subarrays if left boundary expanded
                if left < right:
                    window_len = right - left
                    total -= window_len * (window_len + 1) // 2

        # Add subarrays from final window
        window_len = right - left + 1
        total += window_len * (window_len + 1) // 2

        return total