Problem of The Day: Longest Strictly Increasing or Strictly Decreasing Subarray

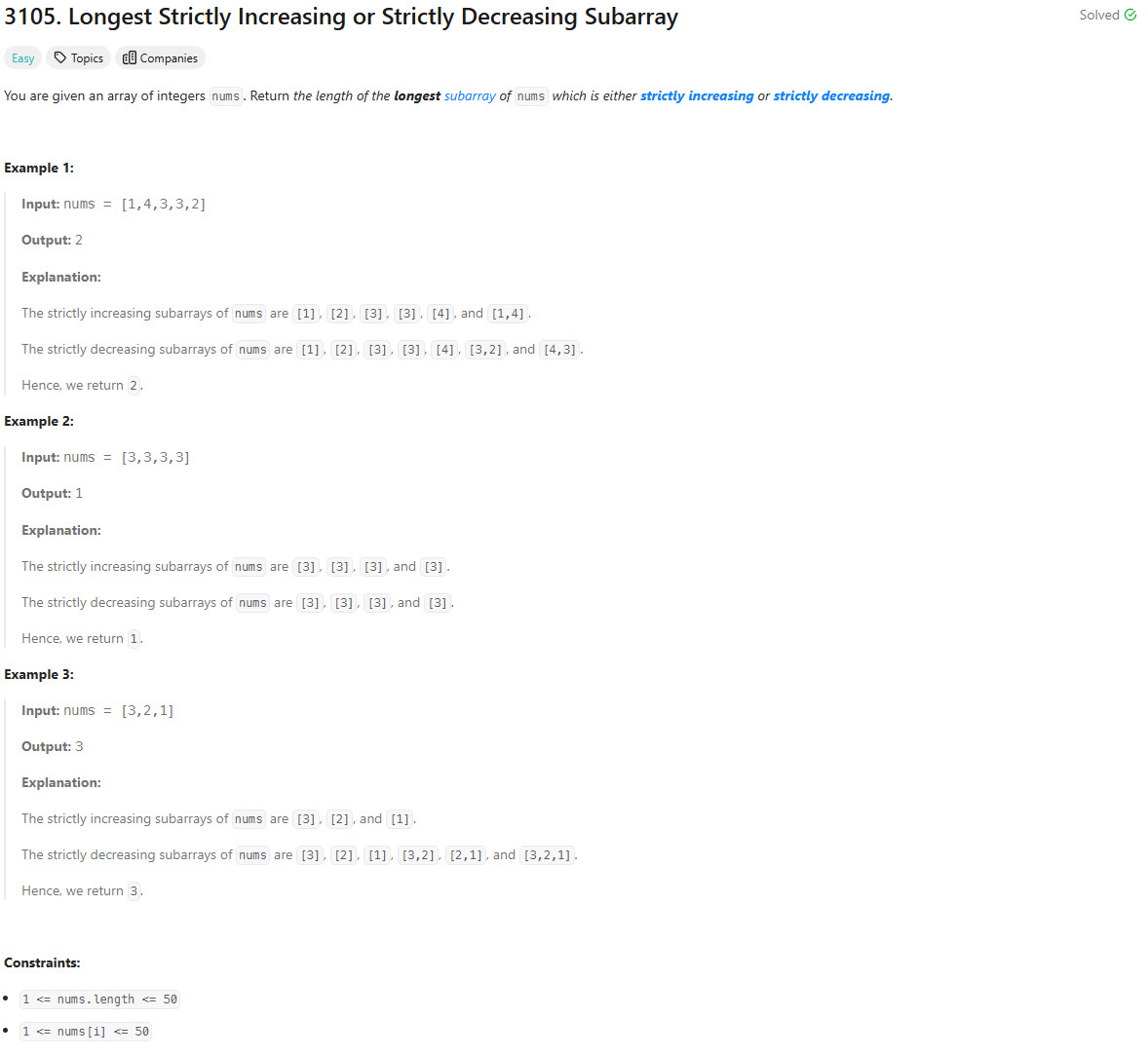
Problem Statement

Sliding Window [Accepted]

class Solution:
    def longestMonotonicSubarray(self, nums: List[int]) -> int:
        start = 0
        N = len(nums)
        res = 0
        for end in range(N):
            if nums[end - 1] >= nums[end]:
                start = end
            res = max(res, end - start + 1)

        start = 0
        for end in range(N):
            if nums[end - 1] <= nums[end]:
                start = end
            res = max(res, end - start + 1)
        return res

Editorial

Brute Force

class Solution:
    def longestMonotonicSubarray(self, nums: list[int]) -> int:
        max_length = 0

        # Find longest strictly increasing subarray
        for start in range(len(nums)):
            curr_length = 1
            for pos in range(start + 1, len(nums)):
                # Extend subarray if next element is larger
                if nums[pos] > nums[pos - 1]:
                    curr_length += 1
                else:
                    # Break if sequence is not increasing anymore
                    break
            max_length = max(max_length, curr_length)

        # Find longest strictly decreasing subarray
        for start in range(len(nums)):
            curr_length = 1
            for pos in range(start + 1, len(nums)):
                # Extend subarray if next element is smaller
                if nums[pos] < nums[pos - 1]:
                    curr_length += 1
                else:
                    # Break if sequence is not decreasing anymore
                    break
            max_length = max(max_length, curr_length)

        return max_length  # Return the longer of increasing or decreasing sequences

• time: O(n^2)
• space: O(1)

Approach 2: Single Iteration

class Solution:
    def longestMonotonicSubarray(self, nums: list[int]) -> int:
        # Track current lengths of increasing and decreasing sequences
        inc_length = dec_length = max_length = 1

        # Iterate through array comparing adjacent elements
        for pos in range(len(nums) - 1):
            if nums[pos + 1] > nums[pos]:
                # If next element is larger, extend increasing sequence
                inc_length += 1
                dec_length = 1  # Reset decreasing sequence
            elif nums[pos + 1] < nums[pos]:
                # If next element is smaller, extend decreasing sequence
                dec_length += 1
                inc_length = 1  # Reset increasing sequence
            else:
                # If elements are equal, reset both sequences
                inc_length = dec_length = 1

            # Update max length considering both sequences
            max_length = max(max_length, inc_length, dec_length)

        return max_length

• time: O(n)
• space: O(1)