Problem of The Day: Lowest Common Ancestor of Deepest Leaves

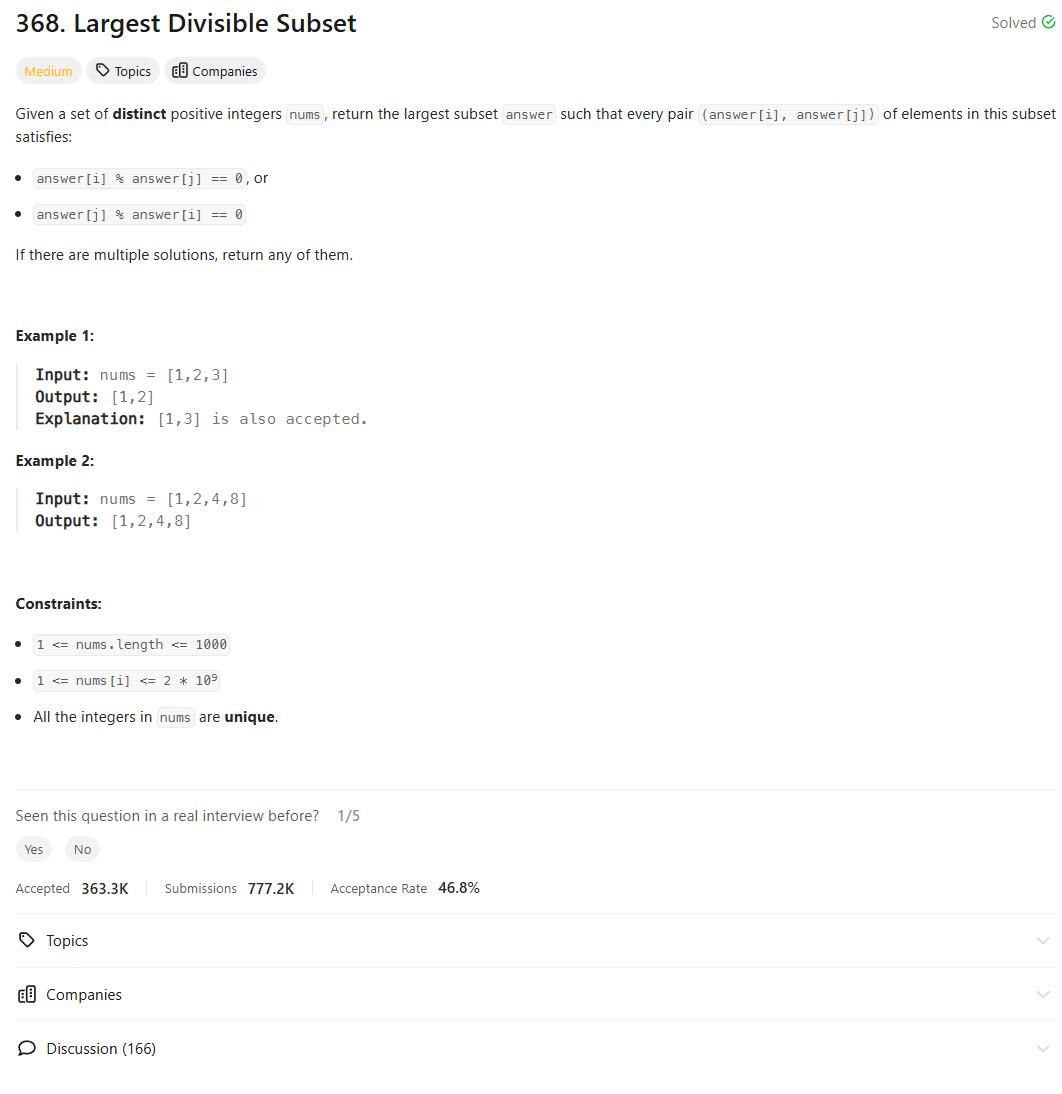
Problem Statement

Brute Force [TLE]

class Solution:
    def largestDivisibleSubset(self, nums: List[int]) -> List[int]:
        N = len(nums)
        res = []
        nums.sort()

        def dfs(start, curr):
            if start == N:
                return curr, len(curr)
            include, len1 = None, 0
            if nums[start] % curr[-1] == 0:
                include, len1 = dfs(start + 1, curr + [nums[start]])
            exclude, len2 = dfs(start + 1, curr)

            if len1 > len2:
                return include, len1
            return exclude, len2


        for i in range(N):
            curr, _ = dfs(i + 1, [nums[i]])
            if len(curr) > len(res):
                res = curr[:]
        return res

Dynamic Programming

class Solution:
    def largestDivisibleSubset(self, nums: List[int]) -> List[int]:
        if not nums:
            return []

        nums.sort()
        n = len(nums)
        dp = [1] * n  # dp[i] = size of the largest subset ending with nums[i]
        prev = [-1] * n  # To reconstruct the subset

        max_len = 0
        max_index = 0

        for i in range(n):
            for j in range(i):
                if nums[i] % nums[j] == 0 and dp[j] + 1 > dp[i]:
                    dp[i] = dp[j] + 1
                    prev[i] = j
            if dp[i] > max_len:
                max_len = dp[i]
                max_index = i

        # Reconstruct the largest subset
        res = []
        while max_index != -1:
            res.append(nums[max_index])
            max_index = prev[max_index]

        return res[::-1]