Problem of The Day: Find Largest Value in Each Tree Row

Problem Statement

Intuition

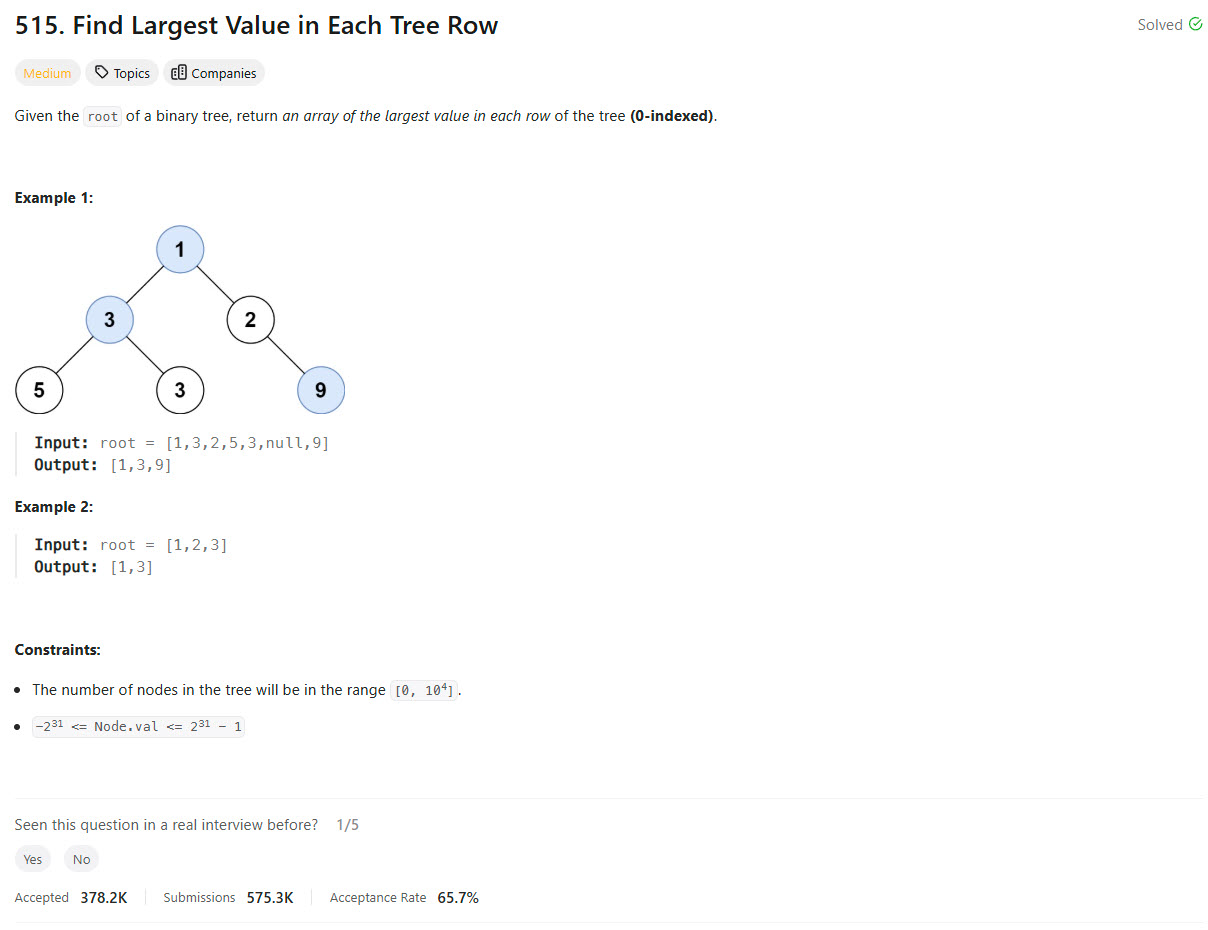
The problem requires finding the largest value in each row of a binary tree. The first thought is to traverse the tree level by level (breadth-first search), keeping track of the largest value encountered at each level.

Approach

1. Use a queue to perform a breadth-first search (BFS) on the tree.
2. At each level:
   • Determine the number of nodes at that level.
   • Iterate through the nodes, keeping track of the maximum value encountered.
   • Add the children of each node to the queue for processing in the next level.
3. Append the maximum value of the current level to the result list.
4. Continue until all levels are processed.
5. Return the result list containing the largest values for each row.

Complexity

• Time complexity:
  \(O(n)\)
  Each node in the tree is visited once, where \(n\) is the number of nodes in the binary tree.

• Space complexity:
  \(O(w)\)
  The space complexity depends on the maximum width of the tree \(w\), which is the maximum number of nodes in any level of the binary tree.

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def largestValues(self, root: Optional[TreeNode]) -> List[int]:
        res = []
        queue = deque([root])
        while queue:
            n = len(queue)
            curr_max = float('-inf')
            for _ in range(n):
                node = queue.popleft()
                if node:
                    curr_max = max(curr_max, node.val)
                    if node.left:
                        queue.append(node.left)
                    if node.right:
                        queue.append(node.right)
            if curr_max != float('-inf'):
                res.append(curr_max)
        return res

Editorial

Approach 1: Breadth First Search (BFS)

class Solution:
    def largestValues(self, root: Optional[TreeNode]) -> List[int]:
        if not root:
            return []

        ans = []
        queue = deque([root])

        while queue:
            current_length = len(queue)
            curr_max = float("-inf")

            for _ in range(current_length):
                node = queue.popleft()
                curr_max = max(curr_max, node.val)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)

            ans.append(curr_max)

        return ans
        ```

Approach 2: Depth First Search (DFS)

class Solution:
    def largestValues(self, root: Optional[TreeNode]) -> List[int]:
        def dfs(node, depth):
            if not node:
                return

            if depth == len(ans):
                ans.append(node.val)
            else:
                ans[depth] = max(ans[depth], node.val)

            dfs(node.left, depth + 1)
            dfs(node.right, depth + 1)

        ans = []
        dfs(root, 0)
        return ans