Problem of The Day: Find Eventual Safe States

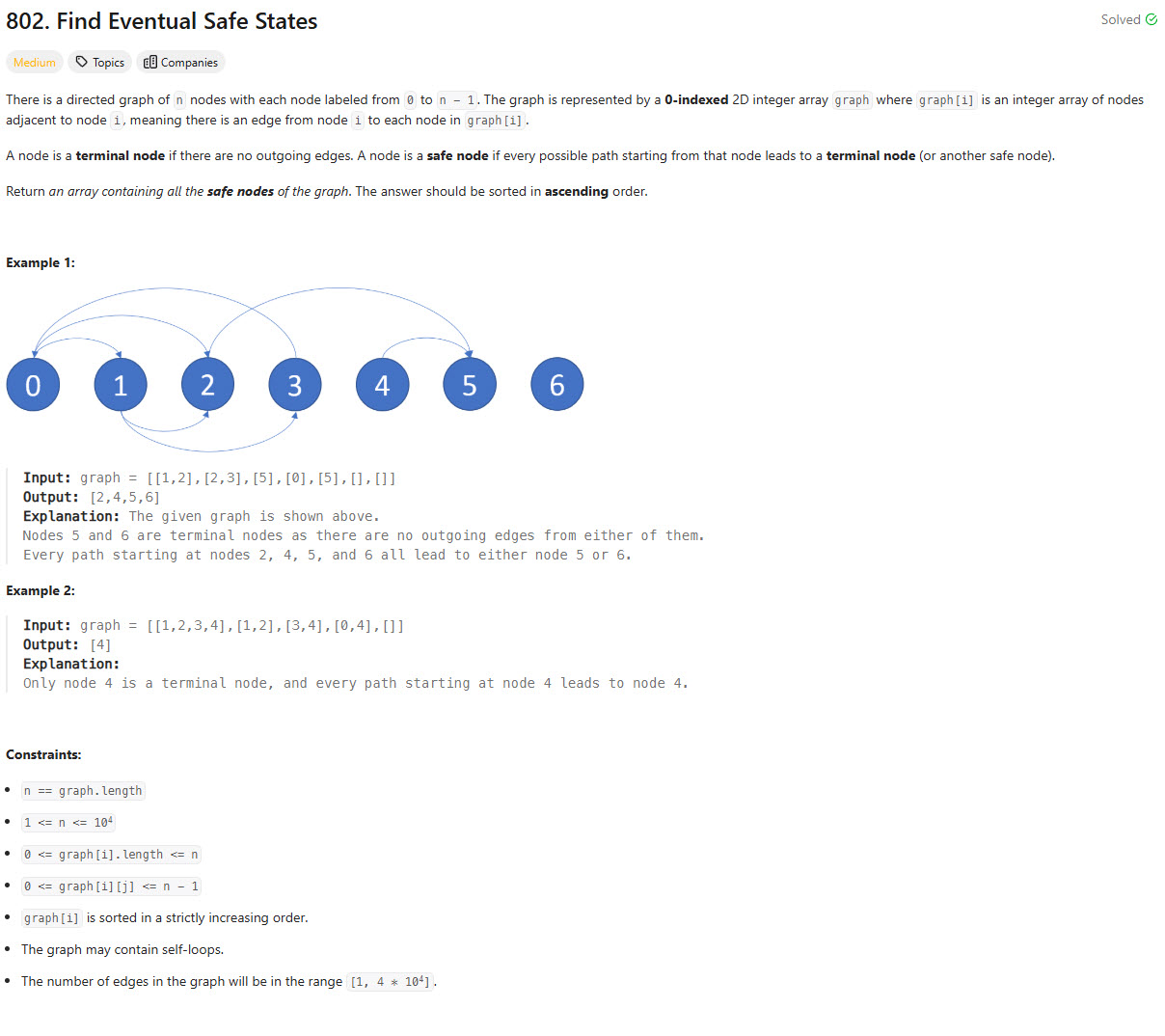
Problem Statement

Brute Force [TLE]

class Solution:
    def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:
        N = len(graph)
        queue = deque()
        safe_nodes = {i: False for i in range(N)}
        adj_list = {i: [] for i in range(N)}

        for i, nodes in enumerate(graph):
            if not nodes:
                queue.append(i)
                safe_nodes[i] = True
            for node in nodes:
                adj_list[node].append(i)

        while queue:
            node = queue.popleft()
            for nei in adj_list[node]:
                if all(safe_nodes[x] for x in graph[nei]):
                    safe_nodes[nei] = True
                    queue.append(nei)

        return [i for i in range(N) if safe_nodes[i]]

Improved Algorithm [Accepted]

N = len(graph)
        # Reverse the graph and calculate outdegrees
        reversed_graph = {i: [] for i in range(N)}
        outdegree = [0] * N

        for u, neighbors in enumerate(graph):
            outdegree[u] = len(neighbors)
            for v in neighbors:
                reversed_graph[v].append(u)

        # Queue for nodes with no outgoing edges (safe nodes)
        queue = deque([i for i in range(N) if outdegree[i] == 0])
        safe_nodes = []

        # Process the queue
        while queue:
            node = queue.popleft()
            safe_nodes.append(node)
            for prev_node in reversed_graph[node]:
                outdegree[prev_node] -= 1
                if outdegree[prev_node] == 0:
                    queue.append(prev_node)

        # Return sorted list of safe nodes
        return sorted(safe_nodes)

Editorial

Approach 1: Topological Sort Using Kahn’s Algorithm

class Solution:
    def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:
        n = len(graph)
        indegree = [0] * n
        adj = [[] for _ in range(n)]

        for i in range(n):
            for node in graph[i]:
                adj[node].append(i)
                indegree[i] += 1

        q = deque()
        # Push all the nodes with indegree zero in the queue.
        for i in range(n):
            if indegree[i] == 0:
                q.append(i)

        safe = [False] * n
        while q:
            node = q.popleft()
            safe[node] = True

            for neighbor in adj[node]:
                # Delete the edge "node -> neighbor".
                indegree[neighbor] -= 1
                if indegree[neighbor] == 0:
                    q.append(neighbor)

        safeNodes = []
        for i in range(n):
            if safe[i]:
                safeNodes.append(i)

        return safeNodes

Approach 2: Depth First Search

class Solution:
    def dfs(self, node, adj, visit, inStack):
        # If the node is already in the stack, we have a cycle.
        if inStack[node]:
            return True
        if visit[node]:
            return False
        # Mark the current node as visited and part of current recursion stack.
        visit[node] = True
        inStack[node] = True
        for neighbor in adj[node]:
            if self.dfs(neighbor, adj, visit, inStack):
                return True
        # Remove the node from the stack.
        inStack[node] = False
        return False

    def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:
        n = len(graph)

        visit = [False] * n
        inStack = [False] * n

        for i in range(n):
            self.dfs(i, graph, visit, inStack)

        safeNodes = []
        for i in range(n):
            if not inStack[i]:
                safeNodes.append(i)

        return safeNodes