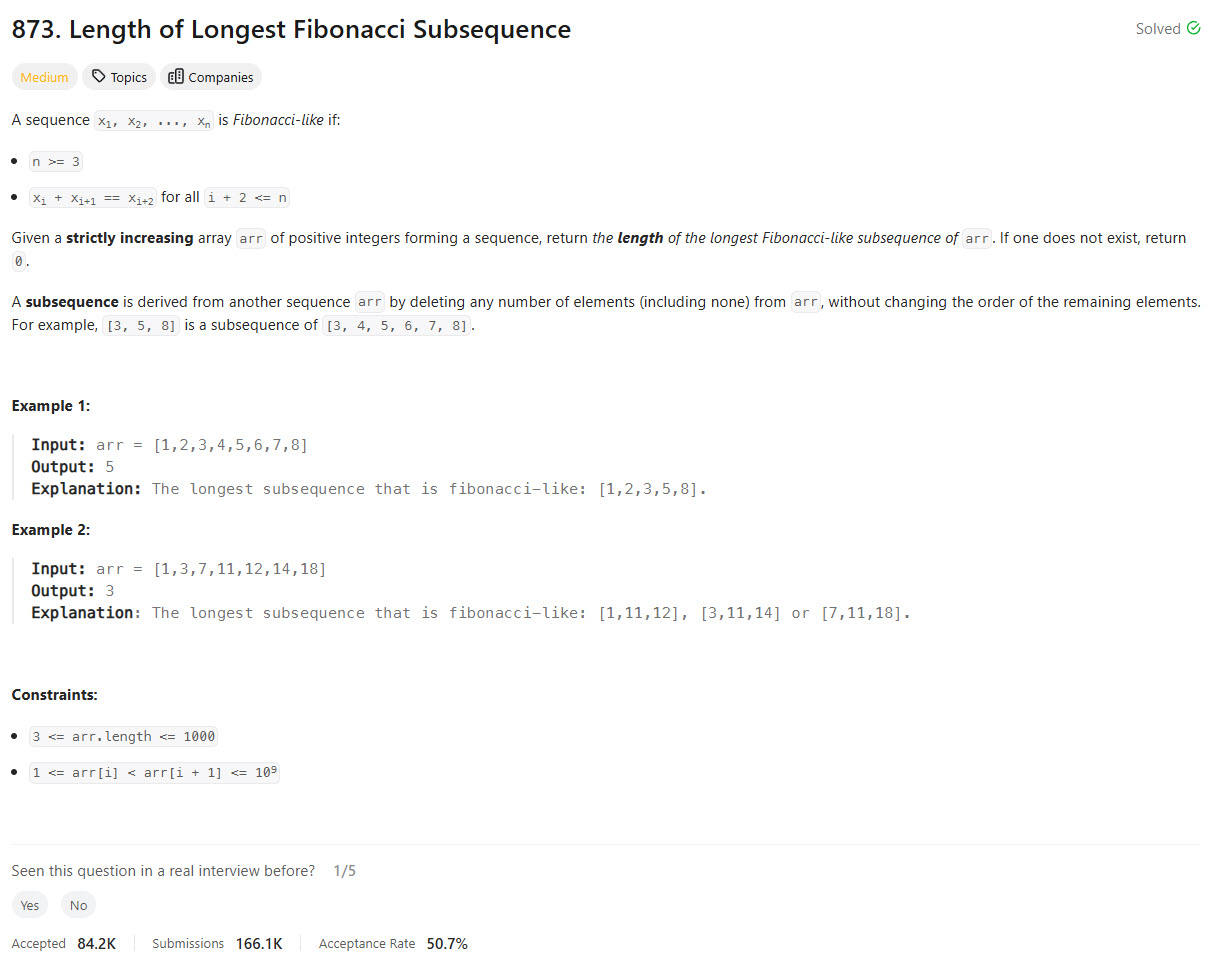
Problem Statement
Brute Force [TLE]
class Solution:
def lenLongestFibSubseq(self, arr: List[int]) -> int:
N = len(arr)
res = 0
for i in range(N):
for j in range(i + 1, N):
if arr[i] + arr[j] in arr:
curr = arr[i]
next_item = arr[j]
count = 2
while curr + next_item in arr:
curr, next_item = next_item, curr + next_item
count += 1
res = max(res, count)
return res
Editorial
Approach 1: Brute Force
class Solution:
def lenLongestFibSubseq(self, arr: list[int]) -> int:
# Store array elements in set for O(1) lookup
num_set = set(arr)
max_len = 0
n = len(arr)
# Try all possible first two numbers of sequence
for start in range(n):
for next in range(start + 1, n):
# Start with first two numbers
prev = arr[next]
curr = arr[start] + arr[next]
curr_len = 2
# Keep finding next Fibonacci number
while curr in num_set:
prev, curr = curr, curr + prev
curr_len += 1
max_len = max(max_len, curr_len)
return max_len
Approach 2: Dynamic Programming
class Solution:
def lenLongestFibSubseq(self, arr: list[int]) -> int:
n = len(arr)
max_len = 0
# dp[prev][curr] stores length of Fibonacci sequence ending at indexes prev,curr
dp = [[0] * n for _ in range(n)]
# Map each value to its index for O(1) lookup
val_to_idx = {num: idx for idx, num in enumerate(arr)}
# Fill dp array
for curr in range(n):
for prev in range(curr):
# Find if there exists a previous number to form Fibonacci sequence
diff = arr[curr] - arr[prev]
prev_idx = val_to_idx.get(diff, -1)
# Update dp if valid Fibonacci sequence possible
# diff < arr[prev] ensures strictly increasing sequence
dp[prev][curr] = (
dp[prev_idx][prev] + 1
if diff < arr[prev] and prev_idx >= 0
else 2
)
max_len = max(max_len, dp[prev][curr])
# Return 0 if no sequence of length > 2 found
return max_len if max_len > 2 else 0
Approach 3: Optimized Dynamic Programming
class Solution:
def lenLongestFibSubseq(self, arr: list[int]) -> int:
n = len(arr)
# dp[prev][curr] stores length of Fibonacci sequence ending at indexes prev,curr
dp = [[0] * n for _ in range(n)]
max_len = 0
# Find all possible pairs that sum to arr[curr]
for curr in range(2, n):
# Use two pointers to find pairs that sum to arr[curr]
start = 0
end = curr - 1
while start < end:
pair_sum = arr[start] + arr[end]
if pair_sum > arr[curr]:
end -= 1
elif pair_sum < arr[curr]:
start += 1
else:
# Found a valid pair, update dp
dp[end][curr] = dp[start][end] + 1
max_len = max(dp[end][curr], max_len)
end -= 1
start += 1
# Add 2 to include first two numbers, or return 0 if no sequence found
return max_len + 2 if max_len else 0
