Problem of The Day: Two Best Non-Overlapping Events

Problem Statement

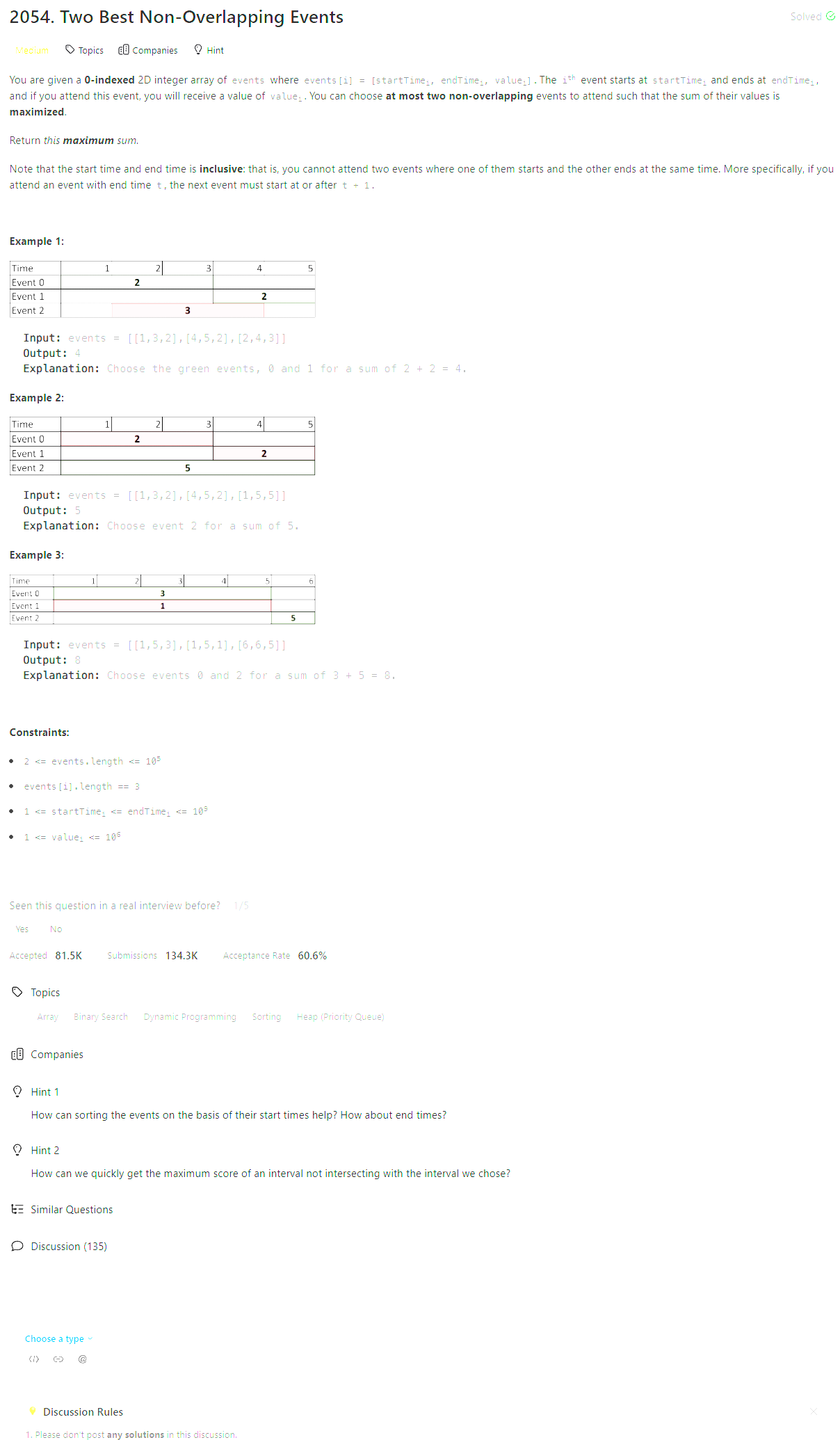
Brute Force [TLE]

class Solution:
    def maxTwoEvents(self, events: List[List[int]]) -> int:
        events.sort()
        N = len(events)
        max_sum = 0
        for i in range(N):
            curr_start, curr_end, curr_val = events[i]
            max_sum = max(max_sum, curr_val)
            for j in range(i + 1, N):
                next_start, next_end, next_val = events[j]
                if next_start > curr_end:
                    max_sum = max(max_sum, curr_val + next_val)
        return max_sum

Editorial

Approach 1: Top-down Dynamic Programming

class Solution:
    def maxTwoEvents(self, events):
        events.sort()
        dp = [[-1] * 3 for _ in range(len(events))]
        return self.find_events(events, 0, 0, dp)

    # Recursive function to find the greatest sum for the pairs.
    def find_events(self, events, idx, cnt, dp):
        if cnt == 2 or idx >= len(events):
            return 0
        if dp[idx][cnt] == -1:
            end = events[idx][1]
            lo, hi = idx + 1, len(events) - 1
            while lo < hi:
                mid = lo + ((hi - lo) >> 1)
                if events[mid][0] > end:
                    hi = mid
                else:
                    lo = mid + 1
            include = events[idx][2] + (
                self.find_events(events, lo, cnt + 1, dp)
                if lo < len(events) and events[lo][0] > end
                else 0
            )
            exclude = self.find_events(events, idx + 1, cnt, dp)
            dp[idx][cnt] = max(include, exclude)
        return dp[idx][cnt]

Approach 2: Min-heap

class Solution:
    def maxTwoEvents(self, events: List[List[int]]) -> int:
        # Create a list to store the pair (end time, value) for events
        pq = []

        # Sort the events by their start time
        events.sort(key=lambda x: x[0])

        max_val = 0
        max_sum = 0

        for event in events:
            # Pop all valid events from the priority queue and take their maximum
            while pq and pq[0][0] < event[0]:
                max_val = max(max_val, pq[0][1])
                heapq.heappop(pq)

            # Calculate the maximum sum by adding the current event's value and the best previous event's value
            max_sum = max(max_sum, max_val + event[2])

            # Push the current event's end time and value into the heap
            heapq.heappush(pq, (event[1], event[2]))

        return max_sum

Approach 3: Greedy

class Solution:
    def maxTwoEvents(self, events):
        times = []
        for e in events:
            # 1 denotes start time.
            times.append([e[0], 1, e[2]])
            # 0 denotes end time.
            times.append([e[1] + 1, 0, e[2]])

        ans, max_value = 0, 0
        times.sort()

        for time_value in times:
            # If current time is a start time, find maximum sum of maximum end
            # time till now.
            if time_value[1]:
                ans = max(ans, time_value[2] + max_value)
            else:
                max_value = max(max_value, time_value[2])

        return ans