Thomas Ngo

Software Engineer

3 minute read

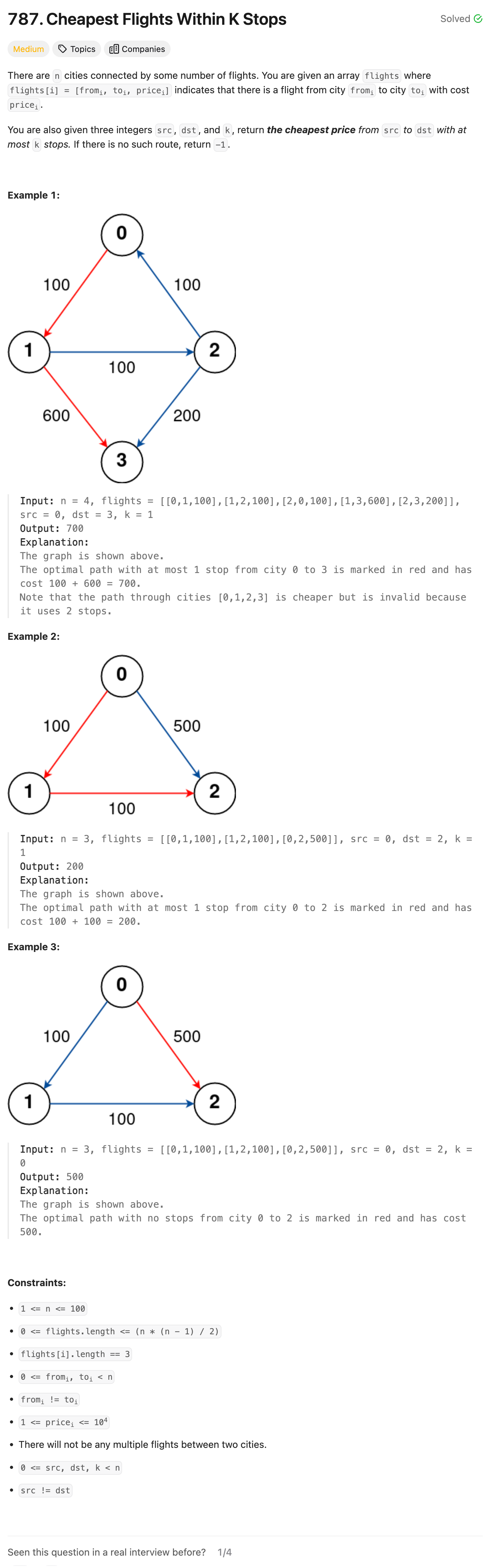
Problem Statement

problem-787

My approach is accepted by Leetcode Judge, but it is quite slow. Need to review the Editorial Solution for more efficient approaches.

Intuition

The problem involves finding the cheapest price to reach the destination with at most k stops. A graph represents cities and flights between them, with associated prices. The intuition is to perform a modified BFS traversal, considering the constraints on the number of stops.

Approach

I’ll create a graph to represent the flights using a defaultdict of lists. Then, I’ll use a deque for BFS traversal. During traversal, I’ll keep track of the total cost and the number of cities visited so far. If the current city is the destination and the number of cities visited is within the limit, I’ll update the result.

I’ll use a defaultdict to keep track of the minimum cost to reach a city. If a city is already visited and the current cost is higher, I’ll skip further exploration for that path.

Complexity

  • Time complexity: O(V + E), where E is the number of flights and V is the number of cities.

  • Space complexity: O(V), where V is the number of cities, for storing the graph and visit information.

Code

class Solution:
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
        graph = defaultdict(list)

        for source, destination, price in flights:
            graph[source].append([destination, price])

        queue = deque()
        queue.append([src, 0, 1])
        res = float('inf')
        visit = defaultdict(int)
        visit[src] = 0

        while queue:
            city, total, num_cities = queue.popleft()
            visit[city] = total
            if city == dst and num_cities - 2 <= k:
                res = min(res, total)

            for dest, price in graph[city]:
                if dest in visit and visit[dest] < total + price:
                    continue
                if price > 0 and num_cities + 1 - 2 <= k:
                    queue.append([dest, total + price, num_cities + 1])


        return res if res != float('inf') else -1

Editorial Solution

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        vector<vector<pair<int, int>>> adj(n);
        for (auto& e : flights) {
            adj[e[0]].push_back({e[1], e[2]});
        }
        vector<int> dist(n, numeric_limits<int>::max());
        queue<pair<int, int>> q;
        q.push({src, 0});
        int stops = 0;

        while (stops <= k && !q.empty()) {
            int sz = q.size();
            // Iterate on current level.
            while (sz--) {
                auto [node, distance] = q.front();
                q.pop();
                // Iterate over neighbors of popped node.
                for (auto& [neighbour, price] : adj[node]) {
                    if (price + distance >= dist[neighbour]) continue;
                    dist[neighbour] = price + distance;
                    q.push({neighbour, dist[neighbour]});
                }
            }
            stops++;
        }
        return dist[dst] == numeric_limits<int>::max() ? -1 : dist[dst];
    }
};
  • Time complexity: O(N + E * K) because the maximum number of times an edge can be processed is limited by K.
  • Space complexity: O(N + E * K)

Approach 2: Bellman Ford

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        // Distance from source to all other nodes.
        vector<int> dist(n, numeric_limits<int>::max());
        dist[src] = 0;

        // Run only K+1 times since we want shortest distance in K hops.
        for (int i = 0; i <= k; i++) {
            // Create a copy of dist vector.
            vector<int> temp(dist);
            for (auto& flight : flights) {
                if (dist[flight[0]] != numeric_limits<int>::max()) {
                    temp[flight[1]] = min(temp[flight[1]], dist[flight[0]] + flight[2]);
                }
            }
            // Copy the temp vector into dist.
            dist = temp;
        }
        return dist[dst] == numeric_limits<int>::max() ? -1 : dist[dst];
    }
};

Approach 3: Dijkstra

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        vector<vector<pair<int, int>>> adj(n);
        for (auto e : flights) {
            adj[e[0]].push_back({e[1], e[2]});
        }
        vector<int> stops(n, numeric_limits<int>::max());
        priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>> pq;
        // {dist_from_src_node, node, number_of_stops_from_src_node}
        pq.push({0, src, 0});

        while (!pq.empty()) {
            auto temp = pq.top();
            pq.pop();
            int dist = temp[0];
            int node = temp[1];
            int steps = temp[2];
            // We have already encountered a path with a lower cost and fewer stops,
            // or the number of stops exceeds the limit.
            if (steps > stops[node] || steps > k + 1) continue;
            stops[node] = steps;
            if (node == dst) return dist;
            for (auto& [neighbor, price] : adj[node]) {
                pq.push({dist + price, neighbor, steps + 1});
            }
        }
        return -1;
    }
};

You may also enjoy