Problem of The Day: Longest Common Subsequence

Problem Statement

Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.

A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.

For example, "ace" is a subsequence of "abcde".
A common subsequence of two strings is a subsequence that is common to both strings.

 

Example 1:

Input: text1 = "abcde", text2 = "ace" 
Output: 3  
Explanation: The longest common subsequence is "ace" and its length is 3.
Example 2:

Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.
Example 3:

Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.
 

Constraints:

1 <= text1.length, text2.length <= 1000
text1 and text2 consist of only lowercase English characters.

My note: Top-down

Bottom-up

My solution

Top-down approach with memoization

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        memo = defaultdict()
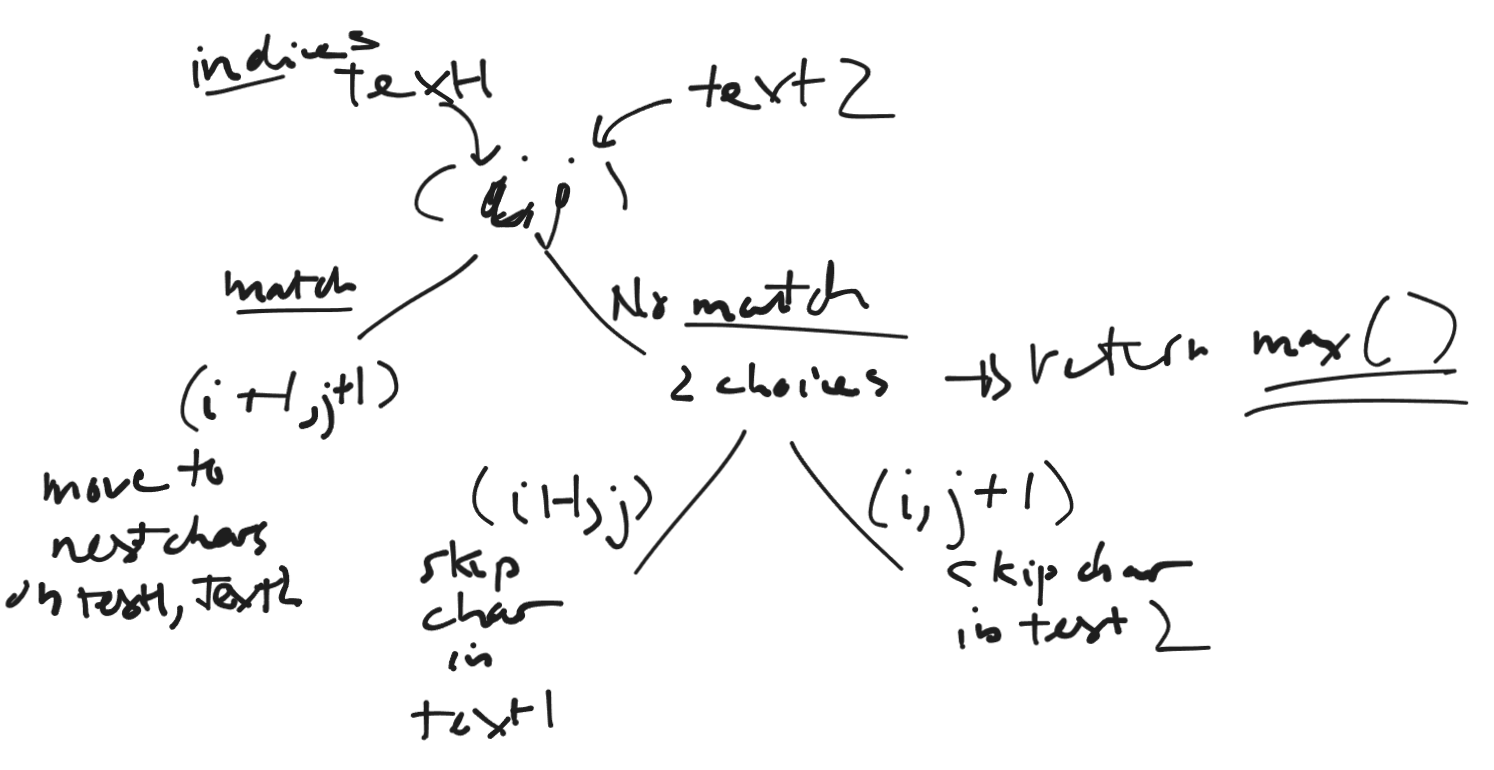
        def dfs(i, j):
            if i == len(text1) or j == len(text2):
                return 0

            if (i, j) in memo:
                return memo[(i, j)]

            if text1[i] == text2[j]:
                return dfs(i + 1, j + 1) + 1

            result = max(dfs(i + 1, j), dfs(i, j + 1))
            memo[(i, j)] = result
            return result

        return dfs(0, 0)

• Time complexity: O(m * n) where m is the length of text1 and n is the length of text2 because there are m * n sub-problems.
• Space complexity: O(m * n) I have already solved this question in the past. Please see this post for my detailed explanation.

Dynamic Programming Approach

In this detailed explanation, the provided solution illustrates the bottom-up approach for solving the longest common subsequence problem. The dp table is populated from the bottom right to the top left. To reinforce my understanding of the problem, I attempted a different implementation by filling the table from the top left to the bottom right. The following Python code demonstrates my approach:

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        m = len(text1)
        n = len(text2)
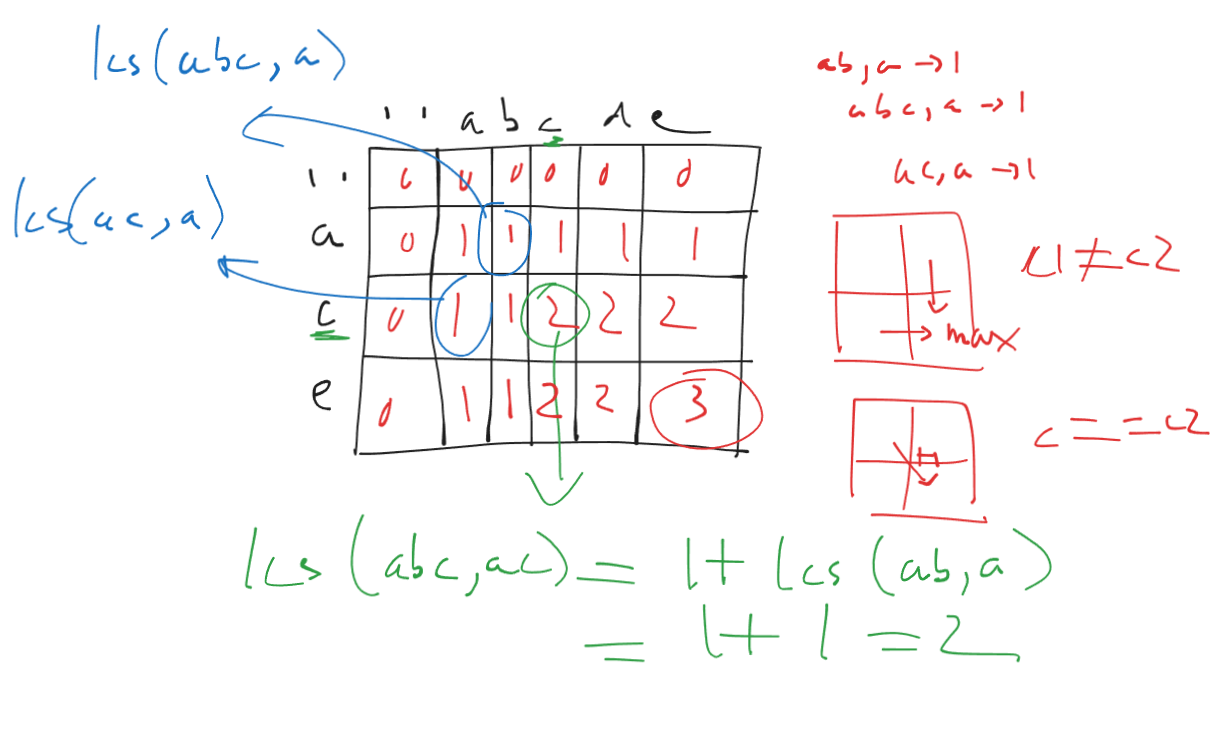
        dp = [[0] * (n + 1) for _ in range(m + 1)]
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                if text1[i - 1] == text2[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1] + 1
                else:
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
        
        return dp[-1][-1]