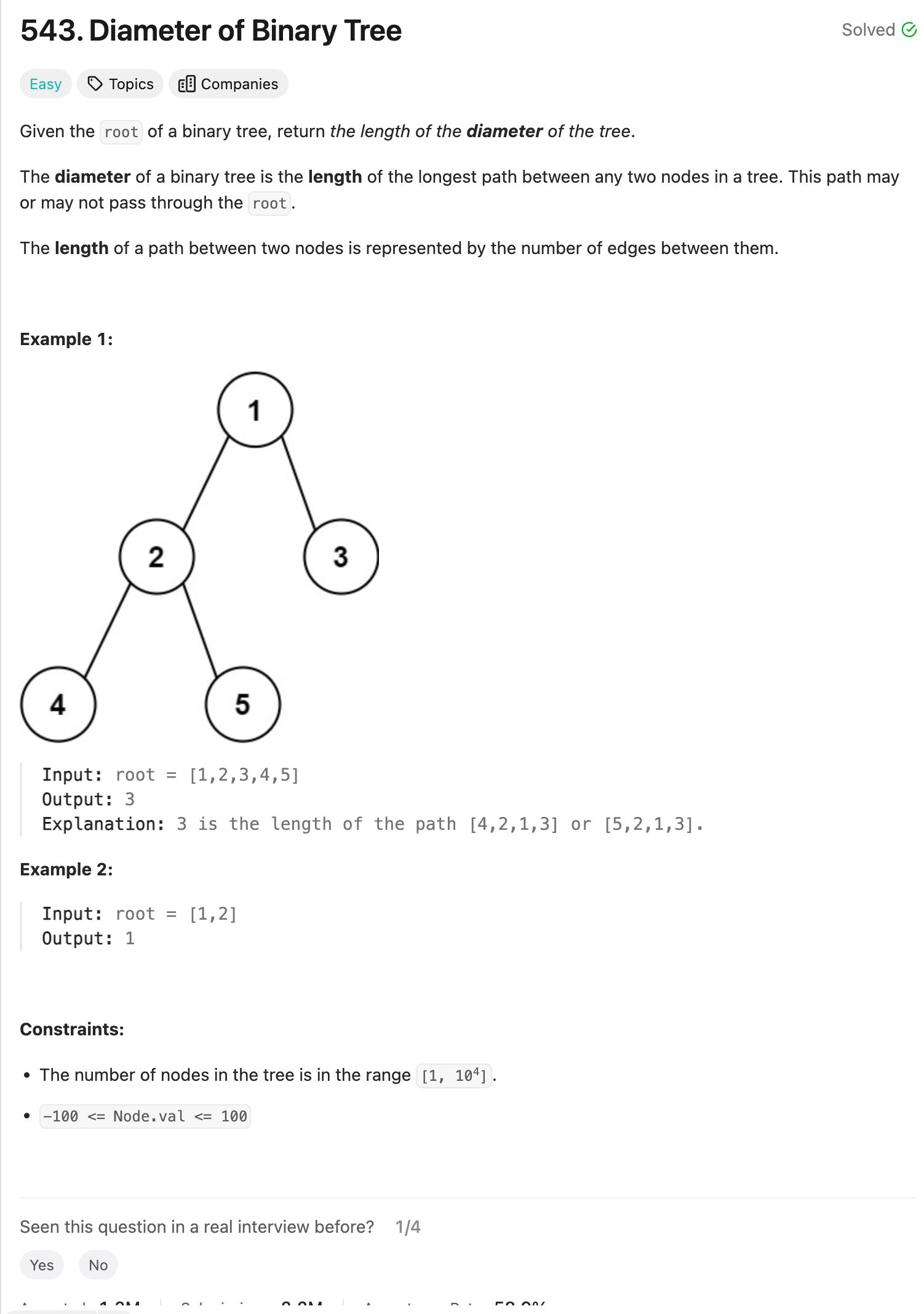
Problem of The Day: Diameter of Binary Tree

Problem Statement

Intuition

To find the diameter of a binary tree, we need to determine the length of the longest path between any two nodes. This path may or may not pass through the root of the tree. The idea is to recursively calculate the depth of the left and right subtrees for each node and keep track of the maximum diameter encountered.

Approach

I will define a recursive helper function that takes a node as input and returns two values - the depth of the subtree rooted at that node and the diameter of the subtree. The depth is the length of the longest path from the node to a leaf. The diameter is the maximum of the following three values:

1. The diameter of the left subtree.
2. The diameter of the right subtree.
3. The sum of depths of the left and right subtrees.

I will use a helper.result variable to keep track of the maximum diameter encountered during the recursion.

Complexity

• Time complexity: O(n) where n is the number of nodes in the binary tree.

• Space complexity: O(n) for the recursion stack. The space required is proportional to the height of the tree, which is O(n) in the worst case.

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        def helper(node):
            if not node:
                return 0, 0
            left_depth, left_diameter = helper(node.left)
            right_depth, right_diameter = helper(node.right)
            helper.result = max(helper.result, left_depth + right_depth)
            return max(left_depth, right_depth) + 1, helper.result

        helper.result = 0
        helper(root)
        return helper.result

Editorial Solution

Approach 1: Depth-first Search

class Solution:
    def diameterOfBinaryTree(self, root: TreeNode) -> int:
        diameter = 0

        def longest_path(node):
            if not node:
                return 0
            nonlocal diameter
            # recursively find the longest path in
            # both left child and right child
            left_path = longest_path(node.left)
            right_path = longest_path(node.right)

            # update the diameter if left_path plus right_path is larger
            diameter = max(diameter, left_path + right_path)

            # return the longest one between left_path and right_path;
            # remember to add 1 for the path connecting the node and its parent
            return max(left_path, right_path) + 1

        longest_path(root)
        return diameter