Problem of The Day: Edit Distance
Problem Statement
Given two strings word1 and word2, return the minimum number of operations required to convert word1 to word2.
You have the following three operations permitted on a word:
Insert a character
Delete a character
Replace a character
Example 1:
Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation:
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
Example 2:
Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation:
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
Constraints:
0 <= word1.length, word2.length <= 500
word1 and word2 consist of lowercase English letters.
Intuition
My initial thoughts to solve this problem involve recursively comparing the characters of the two words and determining the minimum edit distance needed to transform one word into the other. The key operations include insertion, deletion, and replacement of characters.
Approach
I implement a recursive solution using the dfs function. The base cases check if either of the words is empty, in which case the cost is the length of the non-empty word. If the current characters of both words match, no additional cost is incurred, and we move to the next characters. Otherwise, I consider three operations: insert, delete, and replace.
Complexity
-
Time complexity: The time complexity is exponential, as the recursive solution explores all possible combinations of insertions, deletions, and replacements.
-
Space complexity: The space complexity is also exponential, as the recursion stack can grow significantly.
Brute Force - Time Limit Exceeded
using slicing
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
def dfs(w1, w2):
# Base case: If w1 is empty, return the length of w2
if not w1:
# If w1 is empty, inserting each character of w2 is required
return len(w2)
# Base case: If w2 is empty, return the length of w1
if not w2:
# If w2 is empty, deleting each character from w1 is required
return len(w1)
# If the current characters of w1 and w2 are the same,
# move to the next characters without any additional cost
if w1[0] == w2[0]:
return dfs(w1[1:], w2[1:])
# Three possible operations: Insert, Delete, Replace
# Insert: Move to the next character in w2
insert = dfs(w1, w2[1:])
# Delete: Move to the next character in w1
delete = dfs(w1[1:], w2)
# Replace: Move to the next characters in both w1 and w2
replace = dfs(w1[1:], w2[1:])
# Minimum of the three operations plus 1 (cost of the current operation)
return min(insert, delete, replace) + 1
# Start the recursion from the beginning of both words
return dfs(word1, word2)
using indices - set up for memoization
Instead of using slicing in python, I attempted to use the indices. The idea would be the same as the previous section.
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
def dfs(i, j):
# Base case: If w1 is empty, return the length of w2
if i == len(word1):
# If w1 is empty, inserting each character of w2 is required
return len(word2) - j
# Base case: If w2 is empty, return the length of w1
if j == len(word2):
# If w2 is empty, deleting each character from w1 is required
return len(word1) - i
# If the current characters of w1 and w2 are the same,
# move to the next characters without any additional cost
if word1[i] == word2[j]:
return dfs(i + 1, j + 1)
# Three possible operations: Insert, Delete, Replace
# Insert: Move to the next character in w2
insert = dfs(i, j + 1)
# Delete: Move to the next character in w1
delete = dfs(i + 1, j)
# Replace: Move to the next characters in both w1 and w2
replace = dfs(i + 1, j + 1)
# Minimum of the three operations plus 1 (cost of the current operation)
return min(insert, delete, replace) + 1
# Start the recursion from the beginning of both words
return dfs(0, 0)
Memoization
Intuition
The initial intuition remains the same, involving recursively comparing characters and determining the minimum edit distance. To improve the brute force approach, I introduced memoization to store intermediate results and avoid redundant computations.
Approach
I used a dictionary (memo) to store the minimum edit distance for a given pair of indices (i, j) representing the current positions in word1 and word2. If the result for a particular pair has already been calculated, it is retrieved from the memo, reducing the number of recursive calls.
Complexity
-
Time complexity: The time complexity of the dynamic programming solution with memoization can be expressed as
O(m * n), where “m” is the length of word1, and “n” is the length of word2. This is because there are m * n unique index pairs (i, j) for which the minimum edit distance is calculated. The memoization table helps avoid redundant computations and optimizes the overall time complexity. -
Space complexity: The space complexity is also
O(m * n)due to the memoization table. The space required is proportional to the number of unique index pairs (i, j) that are memoized during the recursive calls. Thedefaultdictis used to store the results of subproblems based on the index pairs.
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
memo = defaultdict()
def dfs(i, j):
if i == len(word1):
return len(word2) - j
if j == len(word2):
return len(word1) - i
if (i, j) in memo:
return memo[(i, j)]
if word1[i] == word2[j]:
return dfs(i + 1, j + 1)
insert = dfs(i, j + 1)
delete = dfs(i + 1, j)
replace = dfs(i + 1, j + 1)
result = min(insert, delete, replace) + 1
memo[(i, j)] = result
return result
return dfs(0, 0)
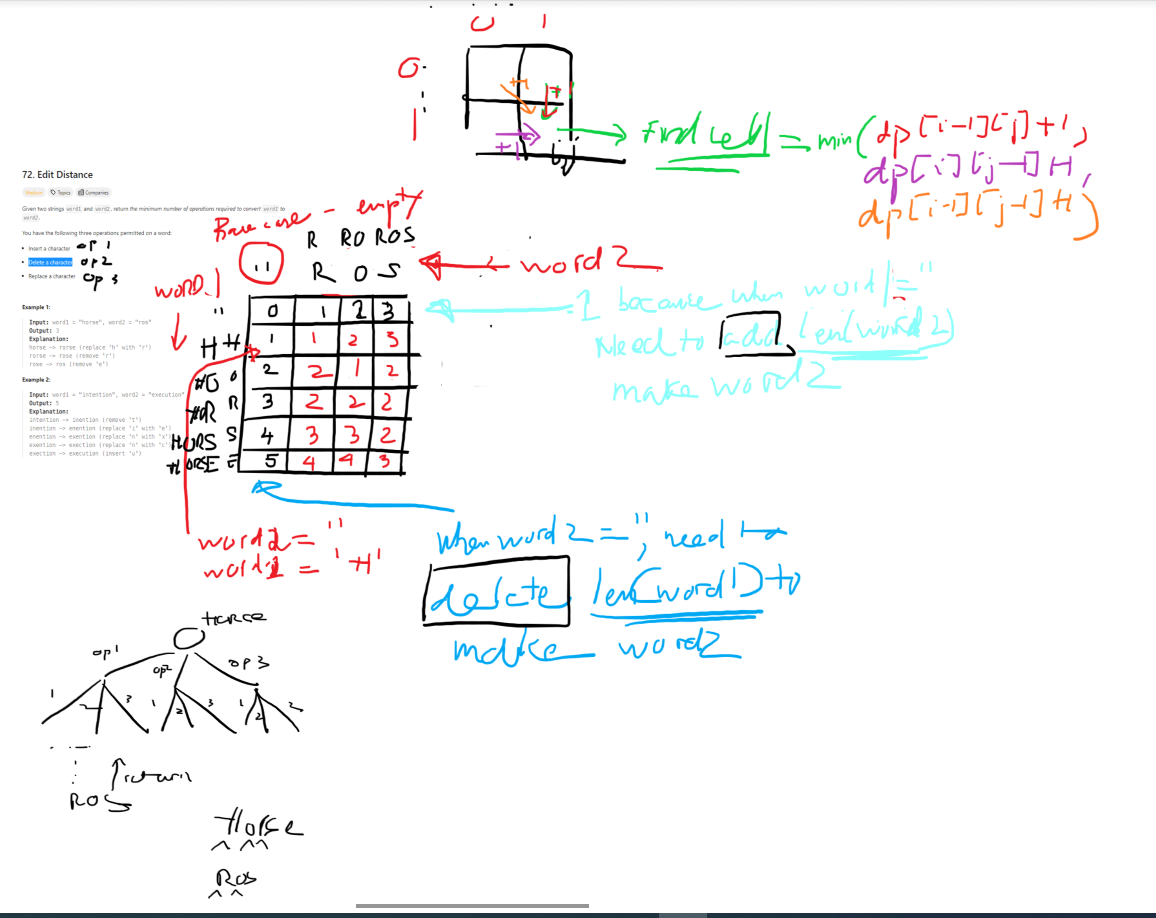
Dynamic Programming
The algorithm constructs a 2D table (dp) where each cell represents the minimum edit distance between the corresponding substrings of word1 and word2. The initialization of the table ensures that the first row and column reflect cumulative lengths of characters in the respective words.
The core of the algorithm lies in filling the DP table by iteratively considering each pair of characters from word1 and word2. If the characters match, the algorithm simply copies the value from the diagonal cell (representing the minimum edit distance without the current characters). In case of a mismatch, the algorithm calculates the minimum cost among three possible operations: insertion, deletion, and replacement. The final value in the bottom-right cell of the DP table gives the minimum edit distance between the entire words.
This dynamic programming approach avoids redundant computations by solving subproblems iteratively and efficiently computes the minimum edit distance. The algorithm’s time complexity is proportional to the product of the lengths of word1 and word2.
Time complexity: O(m * n), where m and n are the lengths of the input words word1 and word2
Space complxity: O(m * n)
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
m, n = len(word1), len(word2)
# Create a 2D DP table with dimensions (m+1) x (n+1)
dp = [[0] * (n + 1) for _ in range(m + 1)]
# Initialize the DP table for base cases
for i in range(m + 1):
dp[i][0] = i
for j in range(n + 1):
dp[0][j] = j
# Fill the DP table using bottom-up dynamic programming
for i in range(1, m + 1):
for j in range(1, n + 1):
# If the current characters match, no additional cost
if word1[i - 1] == word2[j - 1]:
dp[i][j] = dp[i - 1][j - 1]
else:
# Three possible operations: Insert, Delete, Replace
# Choose the minimum cost among the three operations
dp[i][j] = min(dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1]) + 1
# The bottom-right cell of the DP table contains the minimum edit distance
return dp[m][n]
Final state
| r | o | s | ||
|---|---|---|---|---|
| 0 | 1 | 2 | 3 | |
| h | 1 | 1 | 2 | 3 |
| o | 2 | 2 | 1 | 2 |
| r | 3 | 3 | 2 | 2 |
| s | 4 | 4 | 3 | 2 |
| e | 5 | 5 | 4 | 3 |