Problem of The Day: Diameter of Binary Tree

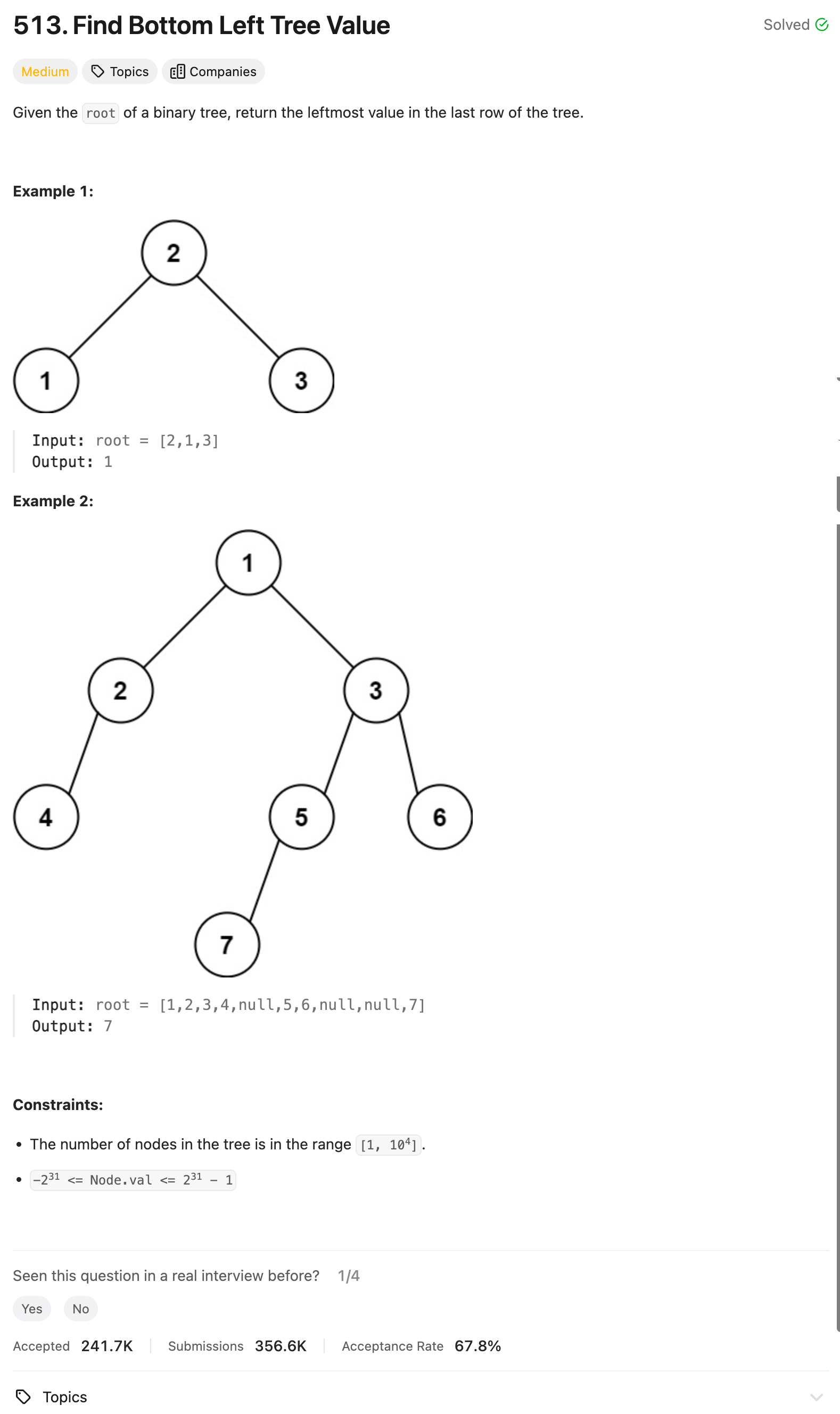
Problem Statement

Intuition

My initial thought is to perform a level-order traversal of the tree using a queue and keep track of the leftmost node at each level.

Approach

I will use a queue to perform level-order traversal. At each level, I will update the leftmost node, and after the traversal, the leftmost node in the bottom level will be the result.

Complexity

• Time complexity: O(n) where n is the number of nodes in the binary tree. We visit each node once.

• Space complexity: O(w) where w is the maximum width of the tree (maximum number of nodes at any level). In the worst case, the queue can contain all nodes at the last level, so the space complexity is proportional to the width of the tree.

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
        queue = deque()
        queue.append(root)
        res = root
        while queue:
            N = len(queue)
            for i in range(N):
                node = queue.popleft()
                if i == 0:
                    res = node
                if node:
                    if node.left:
                        queue.append(node.left)
                    if node.right:
                        queue.append(node.right)
        
        return res.val
                

Editorial Solution

Approach 1: Depth-First Search

class Solution:
    def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
        self.maxDepth = -1
        self.bottomLeftValue = 0
        self.dfs(root, 0)
        return self.bottomLeftValue

    def dfs(self, current: TreeNode, depth: int):
        if not current:
            return
        
        if depth > self.maxDepth:  # If true, we discovered a new level
            self.maxDepth = depth
            self.bottomLeftValue = current.val

        self.dfs(current.left, depth + 1)
        self.dfs(current.right, depth + 1)
        return

Approach 2: Breadth-First Search Right to Left

class Solution:
    def findBottomLeftValue(self, root):
        queue = deque()
        current = root
        queue.append(current)

        while queue:
            current = queue.popleft()

            if current.right:
                queue.append(current.right)

            if current.left:
                queue.append(current.left)

        return current.val