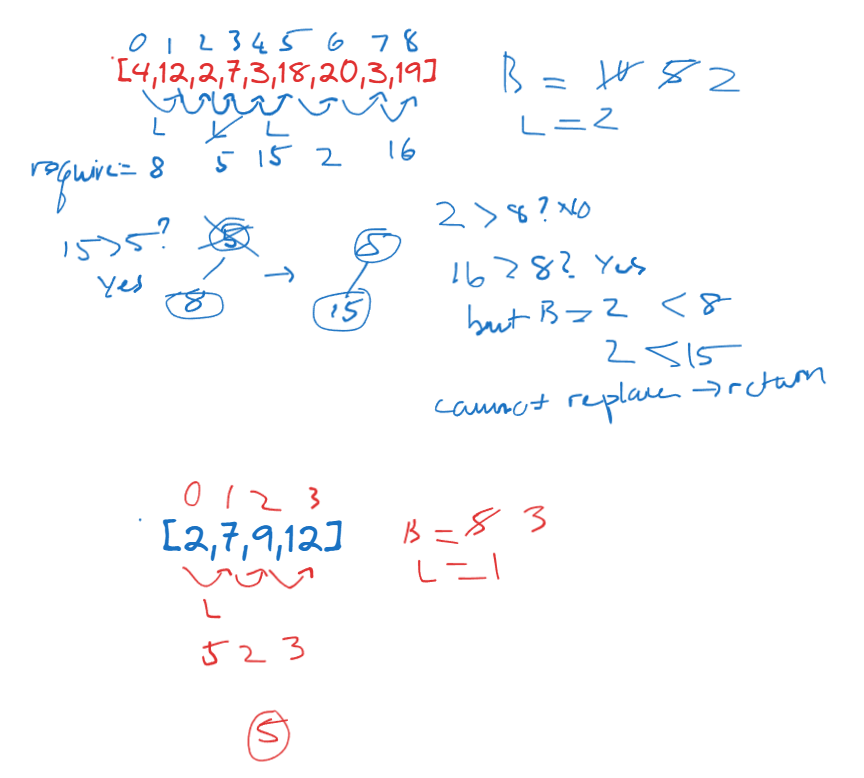Problem of The Day: Furthest Building You Can Reach

Problem Statement

My note:

Intuition

My initial thought is to use a greedy approach, where we prioritize using ladders for the steepest climbs and fall back to bricks when necessary.

Approach

I’ll iterate through the buildings, comparing the heights of consecutive buildings. If the next building is taller, I’ll calculate the difference in height. If I have ladders available, I’ll use one for this climb. If not, I’ll use bricks. In case I’ve used up all ladders, and I need to use bricks, I’ll check if I can replace the previously used bricks with the current climb using a ladder. I’ll keep track of the required bricks in a min heap to efficiently replace the smallest climb if needed.

If at any point I can’t proceed due to insufficient resources (both ladders and bricks), I’ll return the index of the last successfully climbed building.

Complexity

• Time complexity: O(N log k), where N is the number of buildings and k is the number of ladders used. The heapq operations have a logarithmic complexity.

• Space complexity: O(k), where k is the number of ladders used, as we maintain a heap for required bricks.

Code

class Solution:
    def furthestBuilding(self, heights: List[int], bricks: int, ladders: int) -> int:
        N = len(heights)
        required_bricks = [] # min heap
        for i in range(N - 1):
            if heights[i] < heights[i + 1]:
                difference = heights[i + 1] - heights[i]

                if ladders > 0:
                    ladders -= 1
                    heapq.heappush(required_bricks, difference)
                else:
                    if required_bricks and required_bricks[0] < difference:
                        min_height = heapq.heappop(required_bricks)
                        bricks -= min_height
                        heapq.heappush(required_bricks, difference)
                    else:
                        bricks -= difference

                if ladders <= 0 and bricks < 0:
                    return i

        return N - 1