Problem of The Day: Longest Increasing Subsequence
Problem Statement
Given an integer array nums, return the length of the longest strictly increasing subsequence.
Example 1:
Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.
Example 2:
Input: nums = [0,1,0,3,2,3]
Output: 4
Example 3:
Input: nums = [7,7,7,7,7,7,7]
Output: 1
Constraints:
1 <= nums.length <= 2500
-104 <= nums[i] <= 104
Follow up: Can you come up with an algorithm that runs in O(n log(n)) time complexity?
Brute Force- TLE
Intuition
The problem seems to be about finding the length of the Longest Increasing Subsequence (LIS) in a given array. My initial intuition is to use a dynamic programming approach where we can build the solution incrementally.
Approach
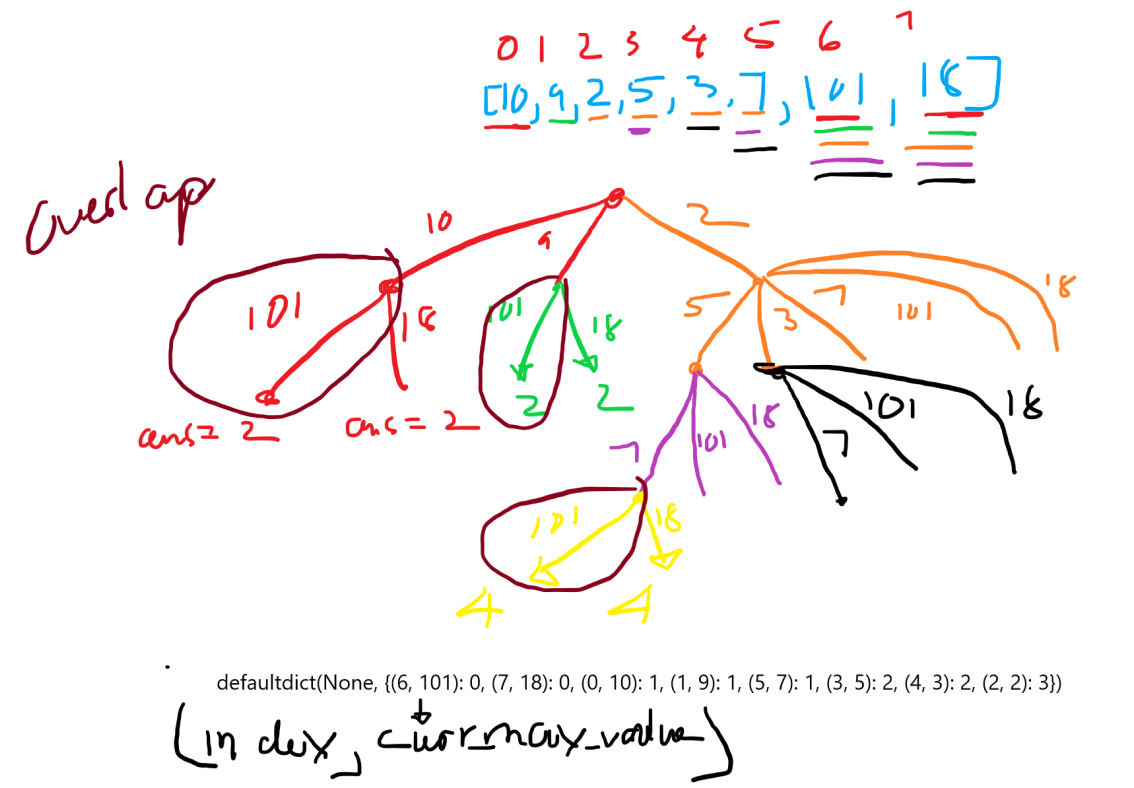
I will implement a recursive function dfs that explores all possible LIS starting from each index in the array. The function will keep track of the current index and the last number in the subsequence. We will increment the length of the subsequence whenever a number greater than the current one is encountered.
I will then iterate through each index in the array and find the maximum length of LIS starting from that index. The final result would be the maximum of all these lengths.
Complexity
- Time complexity: The time complexity of this approach is exponential, specifically O(2^n). This is because for each index, we explore all possible subsequences, leading to repeated computations.
Why 2^n?
In the dfs function, for each index in the array, we explore all possible subsequences by recursively calling the function for the next indices where the current number is less than the subsequent numbers. This branching occurs for each index, leading to an exponential growth in the number of recursive calls.
Let’s analyze the number of recursive calls made:
For the first index, we make calls for the second index, then for the third index, and so on. This leads to 2 recursive calls for the second index (either include or exclude), 2^2 calls for the third index, 2^3 calls for the fourth index, and so forth.
In general, for each index i, there are 2^i recursive calls.
Therefore, the overall number of recursive calls becomes the sum of 2^i for i ranging from 1 to N (the length of the array). This results in exponential time complexity O(2^N).
- Space complexity: The space complexity is also high due to the recursive nature of the solution. It is O(n) as the maximum depth of the recursion can go up to the length of the input array.
Code
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
N = len(nums)
result = 0
def dfs(index, curr_num):
if index == N:
return 0
max_length = 0
for i in range(index + 1, N):
if curr_num < nums[i]:
length = dfs(i, nums[i]) + 1
max_length = max(max_length, length)
return max_length
for i in range(N):
result = max(result, dfs(i, nums[i]) + 1)
return result
Memoization - Top-down
Intuition
In order to improve the brute force approach, I applied memoization to optimize the solution
Approach
I have introduced a memoization mechanism using a defaultdict to store the results of previously computed subproblems. This helps avoid redundant calculations by checking whether the solution for a specific index and current number is already in the memo dictionary before recomputing it.
The memoization enhances the efficiency of the recursive solution by storing and reusing previously computed results, reducing the time complexity.
Complexity
-
Time complexity: The time complexity is improved with memoization, and it becomes O(n^2). This is because, for each index, we still explore all possible subsequences, but the memoization ensures that we don’t recompute solutions for the same subproblems.
-
Space complexity: The space complexity is also reduced due to memoization. It is O(n) as the memo dictionary stores the results for each unique combination of index and current number, limiting the space required compared to the exponential space complexity of the previous solution.
Code
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
N = len(nums)
result = 0
memo = defaultdict()
def dfs(index, curr_num):
if index == N:
return 0
if (index, curr_num) in memo:
return memo[(index, curr_num)]
max_length = 0
for i in range(index + 1, N):
if curr_num < nums[i]:
length = dfs(i, nums[i]) + 1
max_length = max(max_length, length)
memo[(index, curr_num)] = max_length
return max_length
for i in range(N):
result = max(result, dfs(i, nums[i]) + 1)
return result
Dynamic Programming - Bottom-up
Approach
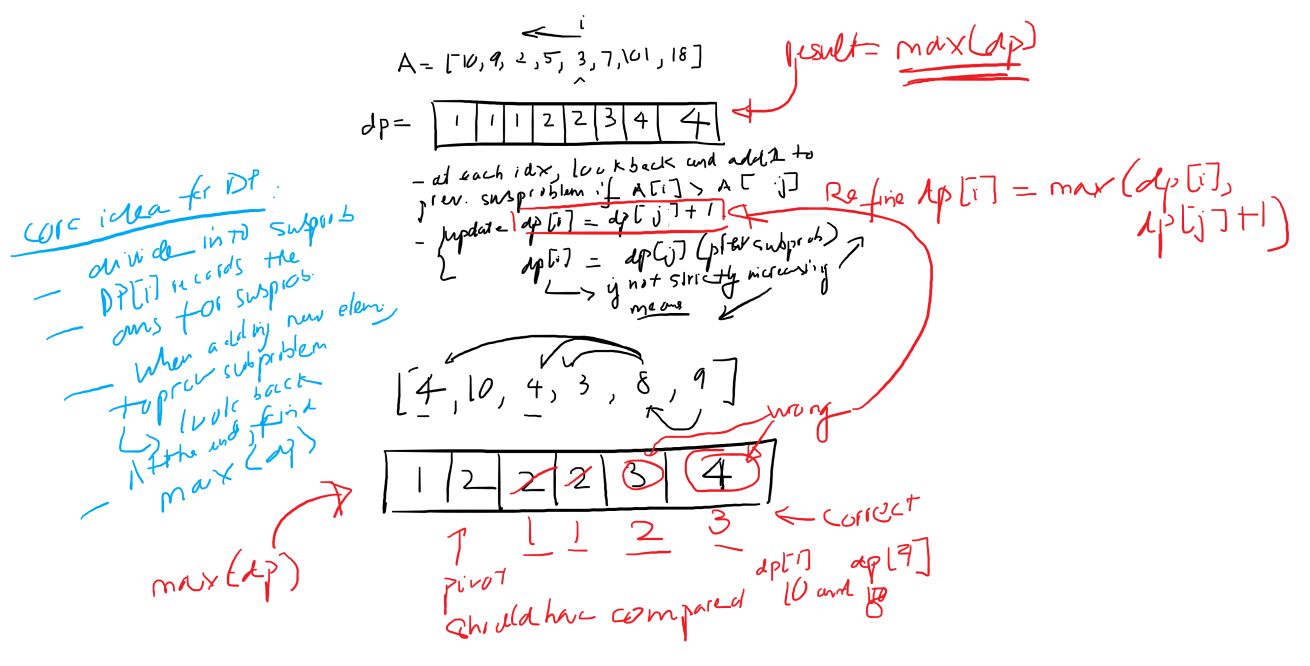
I have adopted a dynamic programming approach using a one-dimensional array dp. The idea is to iterate through each element in the array and, for each element, compare it with the previous elements. If the current element is greater than a previous element, we update the length of the LIS ending at the current index. The final result is the maximum value in the dp array.
This approach avoids the exponential time complexity associated with the recursive solution and its memoized version, making the solution more efficient.
Complexity
-
Time complexity: The time complexity of this dynamic programming solution is O(n^2), where n is the length of the input array. This is because we have nested loops iterating through each element and comparing it with the previous elements.
-
Space complexity: The space complexity is O(n) as we use a one-dimensional array dp to store the length of the LIS ending at each index. The additional space required is proportional to the length of the input array.
Code
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
# Get the length of the input array
N = len(nums)
# Initialize an array to store the length of the LIS ending at each index
dp = [1] * N
# Iterate through each element in the array
for i in range(N):
# Compare the current element with previous elements
for j in range(i):
# If the current element is greater than a previous element
if nums[j] < nums[i]:
# Update the length of the LIS ending at the current index
dp[i] = max(dp[i], dp[j] + 1)
# Return the maximum length of the LIS
return max(dp)
Editorial Solution
Need to review these approaches
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
sub = [nums[0]]
for num in nums[1:]:
if num > sub[-1]:
sub.append(num)
else:
# Find the first element in sub that is greater than or equal to num
i = 0
while num > sub[i]:
i += 1
sub[i] = num
return len(sub)
Time complexity: O(n^2) Space Complexity: O(N)
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
sub = []
for num in nums:
i = bisect_left(sub, num)
# If num is greater than any element in sub
if i == len(sub):
sub.append(num)
# Otherwise, replace the first element in sub greater than or equal to num
else:
sub[i] = num
return len(sub)
Time Complexity: O(n log n) Space Complexity: O(N)