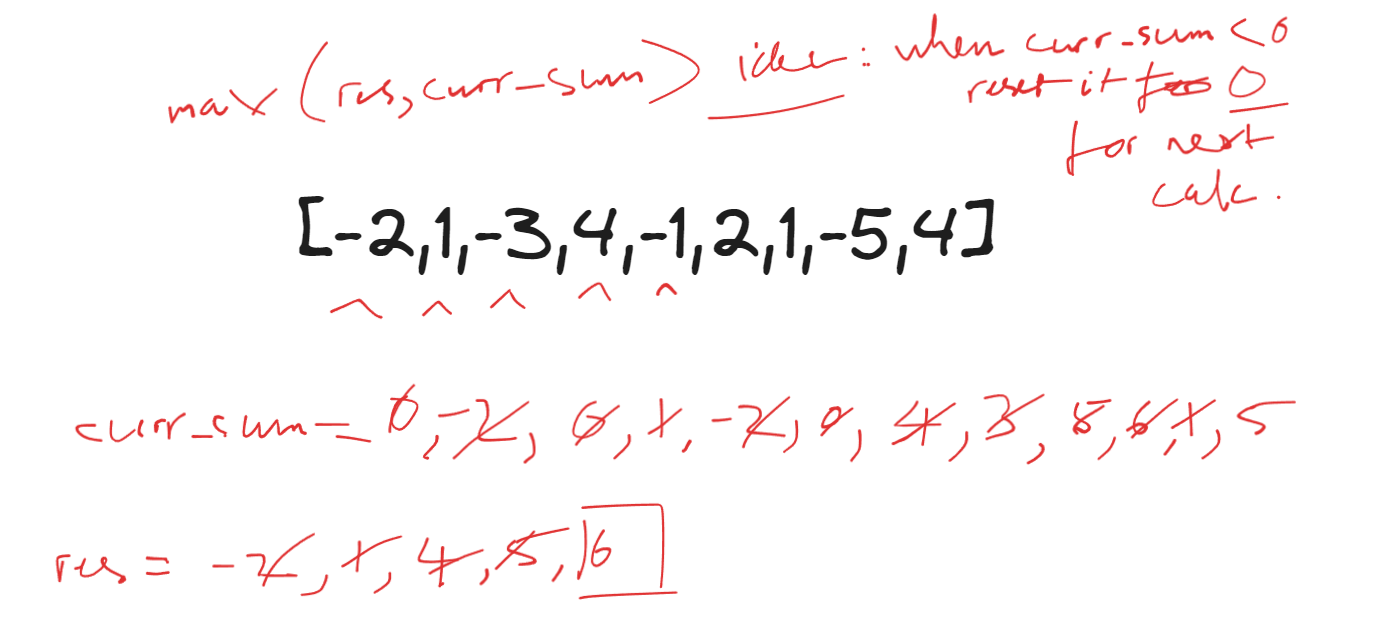Problem of The Day: Maximum Subarray

Problem Statement

Given an integer array nums, find the 
subarray
 with the largest sum, and return its sum.

 

Example 1:

Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: The subarray [4,-1,2,1] has the largest sum 6.
Example 2:

Input: nums = [1]
Output: 1
Explanation: The subarray [1] has the largest sum 1.
Example 3:

Input: nums = [5,4,-1,7,8]
Output: 23
Explanation: The subarray [5,4,-1,7,8] has the largest sum 23.
 

Constraints:

1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4

My note

Intuition

My initial thoughts are to iterate through the array while keeping track of the current sum and updating the maximum sum whenever a new maximum is encountered.

Approach

I will use a variable res to keep track of the maximum sum and another variable curr_sum to store the sum of the current contiguous subarray. I will iterate through the array, update curr_sum by adding each element, and update res whenever a new maximum sum is found. If curr_sum becomes negative, I will reset it to zero since including a negative sum in the subarray would only decrease the total sum.

Complexity

• Time complexity: O(n) where n is the length of the input array, as we iterate through the array once.

• Space complexity: O(1) since we only use a constant amount of extra space (variables res and curr_sum). No additional data structures are used.

Code

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        res = nums[0]
        curr_sum = 0
        for num in nums:
            curr_sum += num
            res = max(res, curr_sum)
            if curr_sum < 0:
                curr_sum = 0
        return res
            

Editorial Solution

Approach 2: Dynamic Programming, Kadane’s Algorithm

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        # Initialize our variables using the first element.
        current_subarray = max_subarray = nums[0]
        
        # Start with the 2nd element since we already used the first one.
        for num in nums[1:]:
            # If current_subarray is negative, throw it away. Otherwise, keep adding to it.
            current_subarray = max(num, current_subarray + num)
            max_subarray = max(max_subarray, current_subarray)
        
        return max_subarray