Problem of The Day: Minimum Falling Path Sum

Problem Statement

Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.

A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).

 

Example 1:
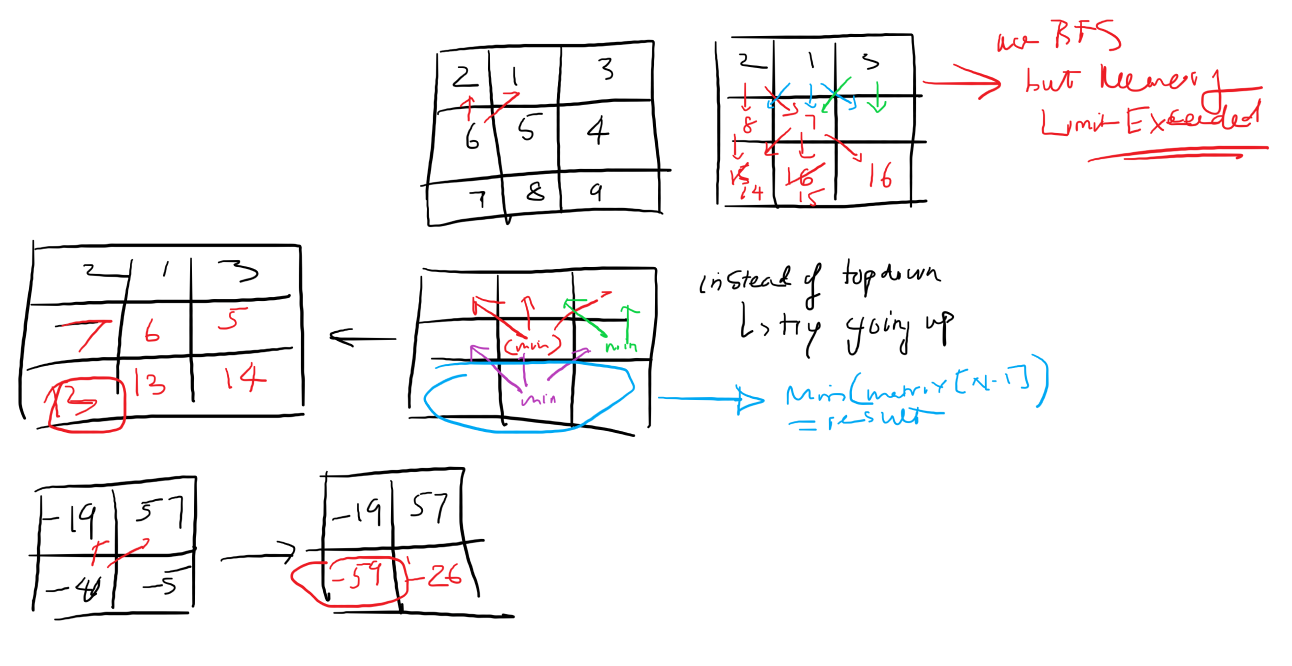
Input: matrix = [[2,1,3],[6,5,4],[7,8,9]]
Output: 13
Explanation: There are two falling paths with a minimum sum as shown.

Example 2:
Input: matrix = [[-19,57],[-40,-5]]
Output: -59
Explanation: The falling path with a minimum sum is shown.

My Note:

Brute Force - Memory Limit Exceeded

Intuition

The problem involves finding the minimum falling path sum in a matrix. My initial thought is to start from the first row and explore all possible paths to reach the bottom row while keeping track of the minimum sum encountered.

Approach

I will use a breadth-first search (BFS) approach to explore different paths. I’ll maintain a queue to traverse through the matrix. At each step, I’ll check the neighboring elements in the next row and update the sum accordingly. The goal is to reach the bottom row and find the minimum falling path sum.

Complexity

• Time complexity: O(N^2), where N is the size of the matrix. In the worst case, we explore all elements of the matrix.

• Space complexity: O(N), as the queue can have at most N elements in the worst case, where N is the number of columns in the matrix.

Code

class Solution:
    def minFallingPathSum(self, matrix: List[List[int]]) -> int:
        res = float('inf')
        N = len(matrix)
        queue = deque()
        for col, x in enumerate(matrix[0]):
            queue.append([0, col, x])
        
        while queue:
            row, col, curr_sum = queue.popleft()
            if row == N - 1:
                res = min(res, curr_sum)
            for col in [col - 1, col, col + 1]:
                if 0 <= col < N and 0 <= row + 1 < N:
                    queue.append([row + 1, col, curr_sum + matrix[row + 1][col]])
        
        return res

Optimized Solution

Intuition

The optimized approach aims to use dynamic programming (DP) to avoid recomputing overlapping subproblems.

Approach

I iterate through each row starting from the second row and update each element with the minimum falling path sum from the previous row. For each element, I consider the three possible choices (left, right, and center) from the row above and choose the one with the minimum sum. This way, I build up the minimum falling path sum for each element in the matrix.

Complexity

• Time complexity: O(N^2), where N is the size of the matrix. In the worst case, we explore all elements of the matrix.

• Space complexity: O(1), as we perform the DP in-place, updating the input matrix without using additional space.

Code

class Solution:
    def minFallingPathSum(self, matrix: List[List[int]]) -> int:
        N = len(matrix)

        for row in range(1, N):
            for col in range(N):
                temp = matrix[row][col]
                val = float('inf') 
                for c in [col - 1, col, col + 1]:
                    if 0 <= c < N:
                        val = min(val, temp + matrix[row - 1][c])
                matrix[row][col] = val

        
        return min(matrix[-1])

Editorial Solution

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) {
        vector<int> dp(matrix.size() + 1, 0);
        for (int row = matrix.size() - 1; row >= 0; row--) {
            vector<int> currentRow(matrix.size() + 1, 0);
            for (int col = 0; col < matrix.size(); col++) {
                if (col == 0) {
                    currentRow[col] =
                        min(dp[col], dp[col + 1]) + matrix[row][col];
                } else if (col == matrix.size() - 1) {
                    currentRow[col] =
                        min(dp[col], dp[col - 1]) + matrix[row][col];
                } else {
                    currentRow[col] =
                        min(dp[col], min(dp[col + 1], dp[col - 1])) +
                        matrix[row][col];
                }
            }
            dp = currentRow;
        }
        int minFallingSum = INT_MAX;
        for (int startCol = 0; startCol < matrix.size(); startCol++) {
            minFallingSum = min(minFallingSum, dp[startCol]);
        }
        return minFallingSum;
    }
};

• Time complexity: O(N^2)
• Space complexity: O(N)