Problem of The Day: Minimum Path Sum
Problem Statement
Intuition
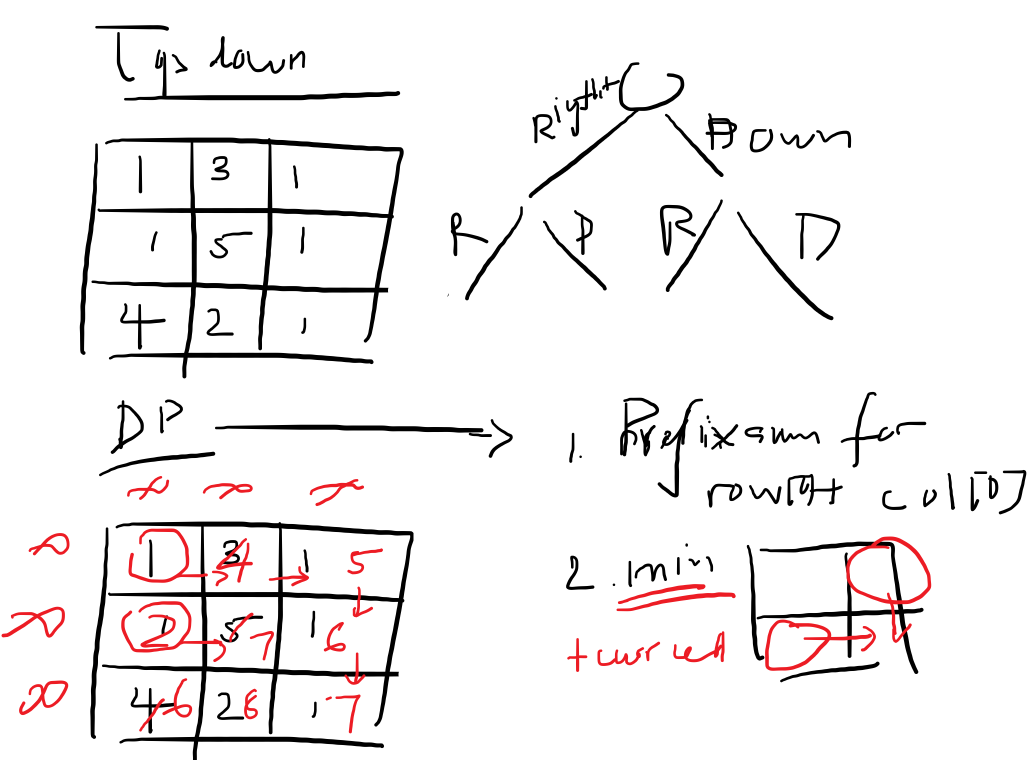
The problem requires finding the minimum path sum from the top-left corner to the bottom-right corner of a grid. The initial approach uses a recursive depth-first search (DFS) to explore all possible paths and calculate the sum for each path.
Approach
The recursive DFS approach explores two directions at each step, moving right and moving down. The function dfs is designed to traverse the grid from the top-left corner to the bottom-right corner, accumulating the current path sum. The minimum path sum is calculated by recursively exploring both right and down directions.
Complexity
-
Time complexity: Exponential, as the algorithm explores all possible paths in the grid.
-
Space complexity: O(m * n), where m is the number of rows and n is the number of columns. This space is used for the call stack in the recursive DFS.
Brute Force - TIME LIMIT EXCEEDED
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
m = len(grid)
n = len(grid[0])
def dfs(row, col, curr_sum):
if row == m or col == n:
return float('inf')
if row == m - 1 and col == n-1:
return curr_sum + grid[row][col]
curr_sum += grid[row][col]
right = dfs(row, col + 1, curr_sum)
down = dfs(row + 1, col, curr_sum)
return min(right, down)
return dfs(0, 0, 0)
Memoization Approach
Use Hash map or Dictionary
The idea is to calculate the minimum path sum for each cell and store the results in a memoization table to avoid redundant calculations.
The approach is to use a recursive function (dfs) that explores all possible paths from a given cell to the destination while memoizing the results. The function calculates the minimum path sum for a cell by considering the sums from the right and down directions. The results are stored in a memoization table to avoid recomputation.
-
Time complexity: O(m×n) - Each cell is visited once, and memoization ensures that each subproblem is solved only once.
-
Space complexity: O(m×n) - The memoization table is used to store the results of subproblems.
from typing import List
from collections import defaultdict
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
m = len(grid)
n = len(grid[0])
def dfs(row, col, memo):
# Base case: if the current position is out of bounds, return infinity
if row == m or col == n:
return float('inf')
# Check if the result for the current cell is already memoized
if (row, col) in memo:
return memo[(row, col)]
# If the current cell is at the bottom-right corner, return its value
if row == m - 1 and col == n - 1:
return grid[row][col]
# Recursively calculate the minimum path sum from the right and down
right = dfs(row, col + 1, memo) + grid[row][col]
down = dfs(row + 1, col, memo) + grid[row][col]
# Calculate the minimum path sum for the current cell
ret_val = min(right, down)
# Memoize the result for the current cell
memo[(row, col)] = ret_val
# Return the minimum path sum for the current cell
return ret_val
# Initialize the memoization table
memo = defaultdict()
# Start the recursive DFS from the top-left corner (row=0, col=0)
return dfs(0, 0, memo)
Use memo as table
Same idea as explained in the previous section. However, we replace the dictionary with table or matrix.
from typing import List
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
m = len(grid)
n = len(grid[0])
# Memoization table to store results of subproblems
memo = [[-1] * n for _ in range(m)]
def dfs(row, col):
# Base case: if the current position is out of bounds, return infinity
if row == m or col == n:
return float('inf')
# If the destination is reached, return the value of the current cell
if row == m - 1 and col == n - 1:
return grid[row][col]
# Check if the result for the current cell is already memoized
if memo[row][col] != -1:
return memo[row][col]
# Recursively calculate the minimum path sum from the right and down
right = dfs(row, col + 1)
down = dfs(row + 1, col)
# Update memoization table with the minimum path sum for the current cell
memo[row][col] = grid[row][col] + min(right, down)
# Return the minimum path sum for the current cell
return memo[row][col]
# Start the recursive DFS from the top-left corner (row=0, col=0)
return dfs(0, 0)
Dynamic Programming Approach
Intuition
Use dynamic programming to efficiently find the minimum path sum in the given grid. The goal is to reach the bottom-right corner of the grid while minimizing the sum of values along the chosen path.
Approach
For this approach, I iterate through the grid and update the values dynamically. I start by updating the values in the first row and first column, as there is only one way to reach any cell in these rows/columns (by moving right or down). Then, for each cell in the remaining rows and columns, I calculate the minimum path sum by considering the values from the cell above and the cell to the left. By iteratively updating the values, the final result is stored in the bottom-right corner.
Complexity
-
Time complexity: O(m x n). I iterate through each cell in the grid once.
-
Space complexity: O(1). I perform the updates in-place without using additional space.
Code
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
m = len(grid)
n = len(grid[0])
# Update values in the first row
for col in range(1, n):
grid[0][col] = grid[0][col] + grid[0][col - 1]
# Update values in the first column
for row in range(1, m):
grid[row][0] = grid[row][0] + grid[row - 1][0]
# Iterate through the remaining cells and update values dynamically
for row in range(1, m):
for col in range(1, n):
grid[row][col] += min(grid[row - 1][col], grid[row][col - 1])
# Return the minimum path sum stored in the bottom-right corner
return grid[-1][-1]