Problem of The Day: Number of Submatrices That Sum to Target
Problem Statement
see problem
Note: This is a very hard problem to solve. Need to review or study the solution for problem 560 in order to internalize the knowledge of prefix sum before attempting to solve this problem. I found this video from NEETCODEIO easy to follow for comprehend the proposed solution.
Need to draw and visualize the problem by hand to fully understand the solution. Need to review this again.
Intuition
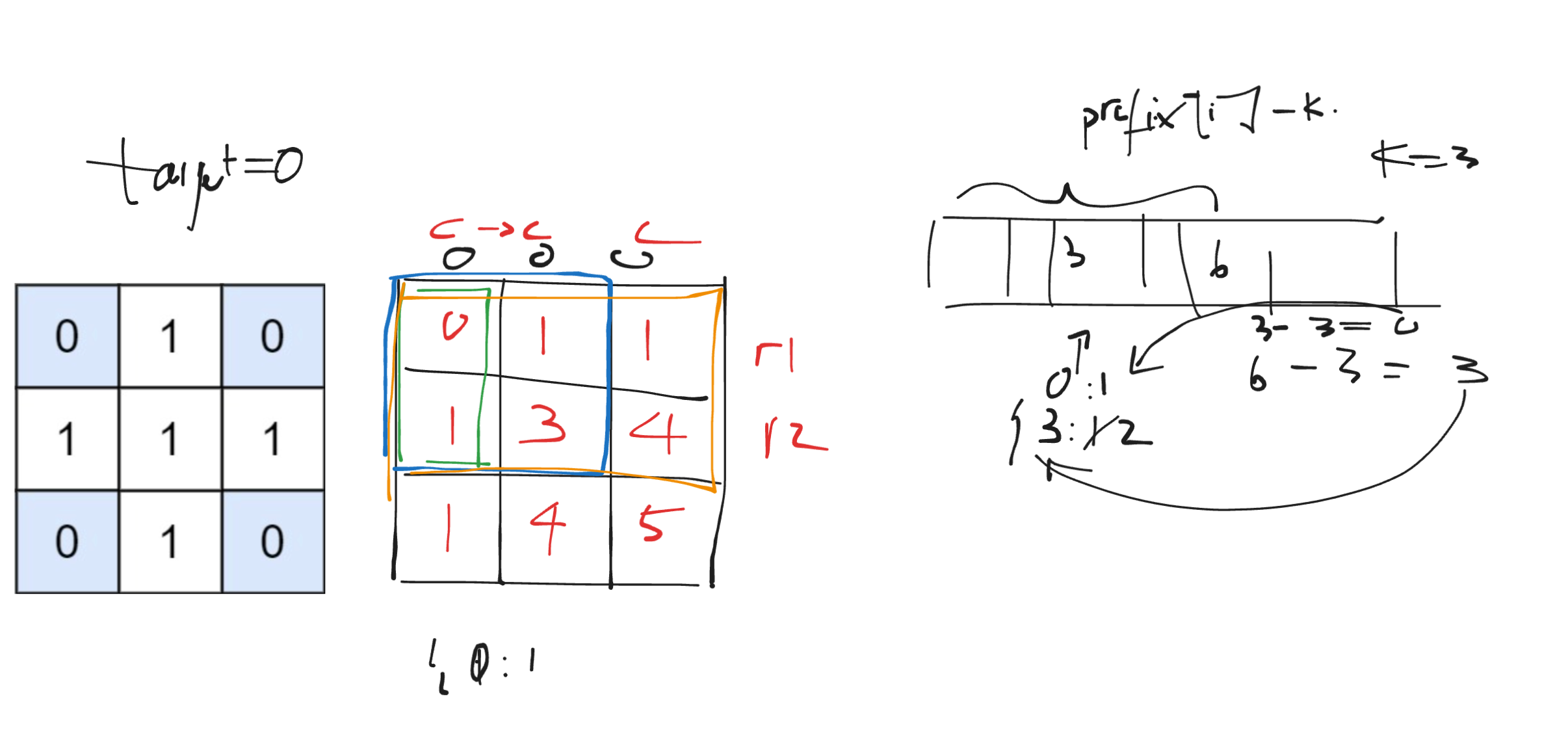
The idea is to leverage prefix sums to efficiently compute submatrix sums. By iterating through the matrix and calculating the prefix sum at each position, the goal is to identify submatrices that sum to the target value.
Approach
The approach involves computing the prefix sum for each element in the matrix. This is done by considering the top, left, and top-left elements at each position. Then, the algorithm iterates through all possible pairs of rows (r1, r2) and maintains a prefix sum for each column. For each column, the current submatrix sum is calculated, and the count of submatrices with the target sum is updated. The algorithm utilizes a prefix dictionary to efficiently track the prefix sums.
Basically, there are 2 main steps to complete in order to solve this question.
Use 2D prefix sum to reduce the problem to lots of smaller 1D problems. Use 1D prefix sum to solve these 1D problems.
Complexity
-
Time complexity:
O(ROWS^2 * COLS), where ROWS is the number of rows in the matrix and COLS is the number of columns. The double nested loops iterate through all possible pairs of rows, and for each pair, there is an additional loop to process each column. -
Space complexity:
O(ROWS * COLS)as the prefix sum information is stored in the matrix itself, and the prefix dictionary has a maximum size of ROWS * COLS.
Code
class Solution:
def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:
ROWS, COLS = len(matrix), len(matrix[0])
# compute prefix sum
for row in range(ROWS):
for col in range(COLS):
top = matrix[row - 1][col] if row - 1 >= 0 else 0
left = matrix[row][col - 1] if col - 1 >= 0 else 0
top_left = matrix[row - 1][col - 1] if row - 1 >= 0 and col - 1 >= 0 else 0
matrix[row][col] = matrix[row][col] + top + left - top_left
res = 0
for r1 in range(ROWS):
for r2 in range(r1, ROWS):
prefix = {0: 1}
for c in range(COLS):
curr_sum = matrix[r2][c] - (matrix[r1 - 1][c] if r1 - 1 >= 0 else 0)
if curr_sum - target in prefix:
res += prefix[curr_sum - target]
prefix[curr_sum] = prefix.get(curr_sum, 0) + 1
return res
Editorial Solution
Approach 1: Number of Subarrays that Sum to Target: Horizontal 1D Prefix Sum
from collections import defaultdict
class Solution:
def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:
r, c = len(matrix), len(matrix[0])
# compute 2D prefix sum
ps = [[0] * (c + 1) for _ in range(r + 1)]
for i in range(1, r + 1):
for j in range(1, c + 1):
ps[i][j] = ps[i - 1][j] + ps[i][j - 1] - ps[i - 1][j - 1] + matrix[i - 1][j - 1]
count = 0
# reduce 2D problem to 1D one
# by fixing two rows r1 and r2 and
# computing 1D prefix sum for all matrices using [r1..r2] rows
for r1 in range(1, r + 1):
for r2 in range(r1, r + 1):
h = defaultdict(int)
h[0] = 1
for col in range(1, c + 1):
# current 1D prefix sum
curr_sum = ps[r2][col] - ps[r1 - 1][col]
# add subarrays which sum up to (curr_sum - target)
count += h[curr_sum - target]
# save current prefix sum
h[curr_sum] += 1
return count
Approach 2: Number of Subarrays that Sum to Target: Vertical 1D Prefix Sum
from collections import defaultdict
class Solution:
def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:
r, c = len(matrix), len(matrix[0])
# compute 2D prefix sum
ps = [[0] * (c + 1) for _ in range(r + 1)]
for i in range(1, r + 1):
for j in range(1, c + 1):
ps[i][j] = ps[i - 1][j] + ps[i][j - 1] - ps[i - 1][j - 1] + matrix[i - 1][j - 1]
count = 0
# reduce 2D problem to 1D one
# by fixing two columns c1 and c2 and
# computing 1D prefix sum for all matrices using [c1..c2] columns
for c1 in range(1, c + 1):
for c2 in range(c1, c + 1):
h = defaultdict(int)
h[0] = 1
for row in range(1, r + 1):
# current 1D prefix sum
curr_sum = ps[row][c2] - ps[row][c1 - 1]
# add subarrays which sum up to (curr_sum - target)
count += h[curr_sum - target]
# save current prefix sum
h[curr_sum] += 1
return count