Problem of The Day: Out of Boundary Paths

Problem Statement

see problem

Intuition

My initial thoughts on solving this problem revolve around the idea of using a recursive approach to explore all possible paths from the starting position within the given maximum number of moves. The goal is to find the number of paths that lead to moving outside the grid.

Approach

I approach this problem by defining a recursive function dfs that explores possible moves in four directions: up, down, left, and right. I keep track of the current position, the remaining moves, and use memoization to avoid redundant calculations. The base cases check whether the current position is outside the grid, and if so, return 1, indicating a valid path. I also handle the case when there are no remaining moves, in which case I return 0. The final result is the sum of valid paths modulo 10^9 + 7.

Complexity

• Time complexity: The time complexity is determined by the number of recursive calls made during the exploration of possible paths. In the worst case, the function explores all possible paths within the given constraints. Therefore, the time complexity can be expressed as O(m * n * maxMove), where m and n are the dimensions of the grid.

• Space complexity: The space complexity is primarily driven by the memoization dictionary, which stores the results of previously calculated subproblems. In the worst case, the memo dictionary can have a size proportional to the number of unique subproblems encountered during the recursive exploration. Therefore, the space complexity can be expressed as O(m * n * maxMove), where m and n are the dimensions of the grid.

Code

class Solution:
    def findPaths(self, m: int, n: int, maxMove: int, startRow: int, startColumn: int) -> int:
        MOD = 10**9 + 7
        memo = defaultdict()
        def dfs(row, col, move):
            if (row < 0 or row >= m) and move >= 0:
                return 1
            if (col < 0 or col >= n) and move >= 0:
                return 1
            if move <= 0:
                return 0

            if (row, col, move) in memo:
                return memo[(row, col, move)]

            res = 0
            for x, y in ([1,0],[-1,0],[0,1],[0,-1]):
                res += dfs(row + x, col + y, move - 1)

            memo[(row, col, move)] = res % MOD
            return res % MOD

        return dfs(startRow, startColumn, maxMove)

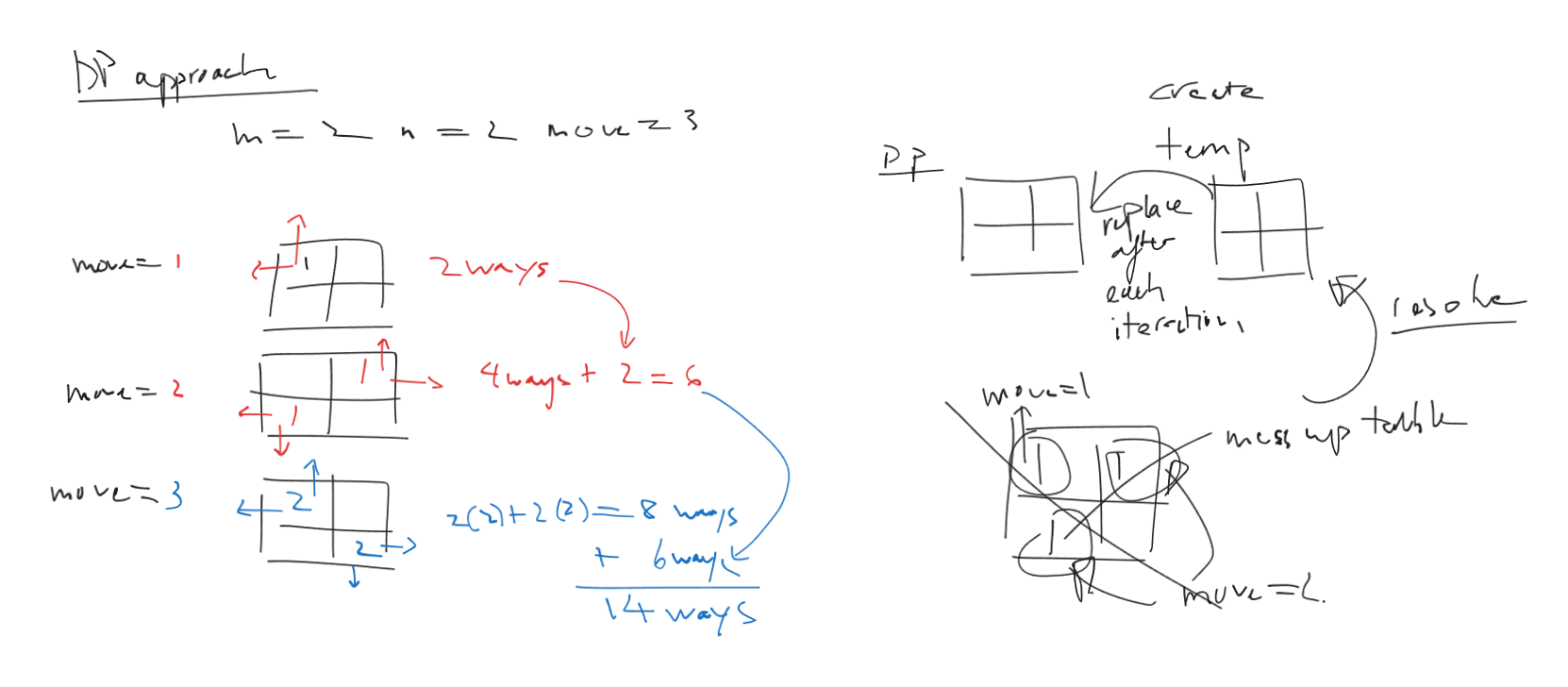
Dynamic Programming Approach

My note:

class Solution:
    def findPaths(self, m, n, N, x, y):
        M = 10**9 + 7
        dp = [[0] * n for _ in range(m)]
        dp[x][y] = 1
        count = 0
        
        for moves in range(1, N + 1):
            temp = [[0] * n for _ in range(m)]
            for i in range(m):
                for j in range(n):
                    if i == m - 1:
                        count = (count + dp[i][j]) % M
                    if j == n - 1:
                        count = (count + dp[i][j]) % M
                    if i == 0:
                        count = (count + dp[i][j]) % M
                    if j == 0:
                        count = (count + dp[i][j]) % M
                    temp[i][j] = (
                        ((dp[i - 1][j] if i > 0 else 0) + (dp[i + 1][j] if i < m - 1 else 0)) % M +
                        ((dp[i][j - 1] if j > 0 else 0) + (dp[i][j + 1] if j < n - 1 else 0)) % M
                    ) % M
            dp = temp
            print(count)
        return count