Problem of The Day: Partition Array for Maximum Sum

Problem Statement

Scratch Notes

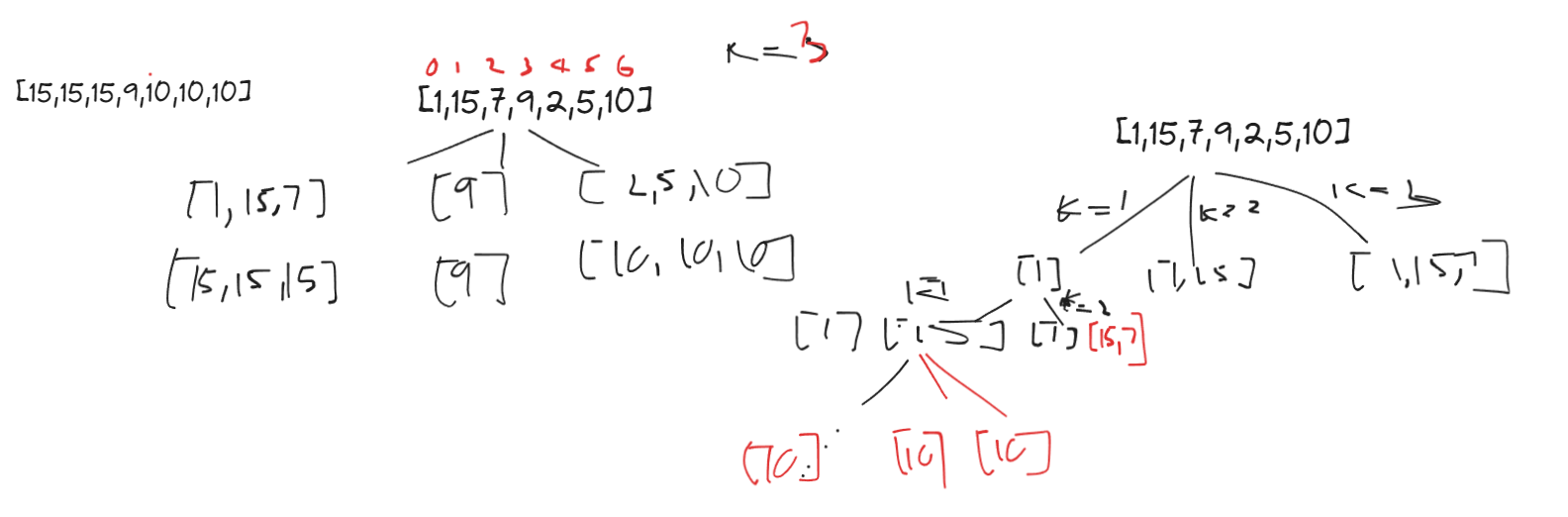
Brute Force - TLE

Attempted to use backtrack to solve

class Solution:
    def maxSumAfterPartitioning(self, arr: List[int], k: int) -> int:
        subarrays_max = []
        N = len(arr)
        def dfs(idx):
            if idx >= N:
                return sum(subarrays_max)

            res = 0
            for i in range(1, k + 1):
                val = max(arr[idx:idx + i])
                for _ in range(len(arr[idx:idx + i])):
                    subarrays_max.append(val)

                res = max(res, dfs(idx + i))

                for _ in range(len(arr[idx:idx + i])):
                    subarrays_max.pop()
            
            return res

        return dfs(0)

Other implementation

class Solution:
    def maxSumAfterPartitioning(self, arr: List[int], k: int) -> int:
        N = len(arr)
        def dfs(idx, curr):

            if idx >= N:
                re = 0
                for subarray in curr:
                    max_val = max(subarray)
                    for _ in range(len(subarray)):
                        re += max_val
                return re

            res = 0
            for i in range(1, k + 1):
                res = max(res, dfs(idx + i, curr + [arr[idx:idx + i]]))

            return res

        return dfs(0, [])

Memoization Approach - Accepted

Intuition

The key idea is likely to consider all possible partitioning strategies and find the one that maximizes the sum.

Approach

The provided code is using a recursive approach with memoization. It defines a function dfs that takes an index i as a parameter, indicating the current position in the array. The function explores all possible partitions by considering subarrays of at most size k, calculating the sum for each partition, and recursively moving to the next position.

The memo dictionary is used to store already computed results for a given index, avoiding redundant calculations.

Complexity

• Time complexity: O(n*k) the function dfs is called for each index from 0 to N-1, and for each call, it explores up to the next k elements.

• Space complexity: The space complexity is determined by the size of the memo dictionary, which is proportional to the number of unique subproblems. In the worst case, it could be O(n), where n is the length of the input array.

Code

class Solution:
    def maxSumAfterPartitioning(self, arr: List[int], k: int) -> int:
        N = len(arr)
        memo = defaultdict()

        def dfs(i):
            if i >= N:
                return 0

            if i in memo:
                return memo[i]

            curr_max = 0
            res = 0

            for j in range(i, min(N, i + k)):
                curr_max = max(curr_max, arr[j])
                window_size = j - i + 1
                res = max(res, curr_max * window_size + dfs(j + 1))

            memo[i] = res
            return res
        return dfs(0)

Editor Solution

Dynamic Programming - 1D array

class Solution:
    def maxSumAfterPartitioning(self, arr: List[int], k: int) -> int:
        N = len(arr)
        dp = [0] * N
        for i in range(N - 1, -1, -1):
            curr_max = 0
            for j in range(i, min(N, i + k)):
                curr_max = max(curr_max, arr[j])
                window_size = j - i + 1
                prev = dp[j + 1] if j + 1 < N else 0
                dp[i] = max(dp[i], curr_max * window_size + prev)
        
        return dp[0]

Dynamic Programming - 1D array fixed K size

The idea is to realize that the 1D dynamic programming approach only use k-size of previous subarray for the current computation. Therefore, we can reduce space by utilizing just k-size array instead of N-size array to cache the previous sub-problem.

class Solution:
    def maxSumAfterPartitioning(self, arr: List[int], k: int) -> int:
        N = len(arr)
        K = k + 1
        dp = [0] * K
        for i in range(N - 1, -1, -1):
            curr_max = 0
            for j in range(i, min(N, i + k)):
                curr_max = max(curr_max, arr[j])
                window_size = j - i + 1
                prev = dp[(j + 1) % K]
                dp[i % K] = max(dp[i % K], curr_max * window_size + prev)
                print(dp)
        return dp[0]