Problem of The Day: Perfect Square

Problem Statement

Given an integer n, return the least number of perfect square numbers that sum to n.

A perfect square is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, 1, 4, 9, and 16 are perfect squares while 3 and 11 are not.

 

Example 1:

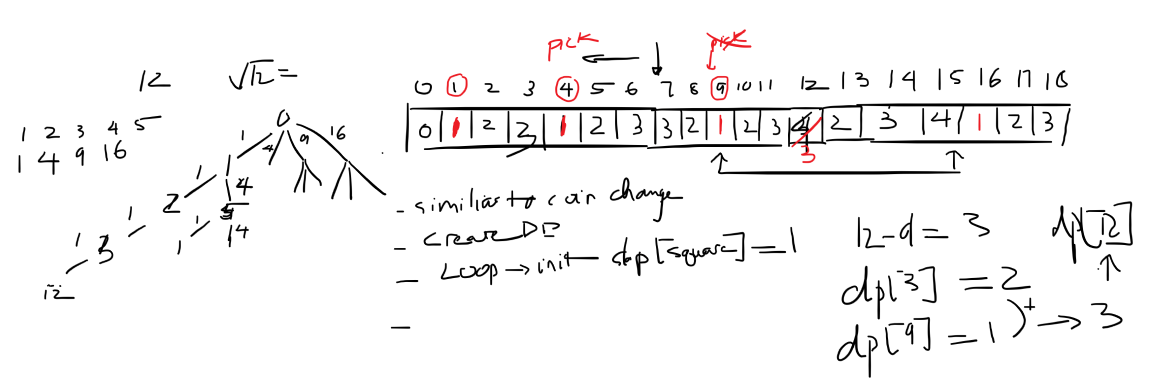
Input: n = 12
Output: 3
Explanation: 12 = 4 + 4 + 4.
Example 2:

Input: n = 13
Output: 2
Explanation: 13 = 4 + 9.
 

Constraints:

1 <= n <= 10^4

My note:

Brute Force - TLE

Intuition

The given problem seems to be a classic dynamic programming challenge involving finding the minimum number of perfect squares that sum up to a given number.

Approach

I’ve defined a recursive function dfs to explore the possibilities of forming 'n' using perfect squares. The function takes two parameters: num (the current number being considered) and curr_sum (the remaining sum to be achieved). The base cases check if curr_sum is 0 or negative. If it’s 0, we’ve successfully formed 'n', and if it’s negative, it’s an invalid path.

The function then iterates through all possible perfect squares less than or equal to the current sum, updating the result by recursively calling the function with the updated parameters.

Complexity

• Time complexity: The time complexity is exponential, specifically O(2^n). This is because for each recursive call, we iterate through all possible perfect squares less than or equal to the current sum.

• Space complexity: The space complexity is O(n), where ‘n’ is the input parameter. This is due to the recursive nature of the solution, leading to a maximum depth of ‘n’ in the call stack.

  class Solution:
    def numSquares(self, n: int) -> int:
        def dfs(num, curr_sum):
            if curr_sum == 0:
                return 0
  
            if curr_sum < 0:
                return float('inf')
  
            result = float('inf')
            for x in range(1, curr_sum + 1):
                square = x **2
                result = min(result, dfs(x, curr_sum - square) + 1)
  
            return result
  
        return dfs(0, n)
  

Memoization - TLE

To improve the brute force approach, I attempted to use memoization method.

• Time complexity: The time complexity is improved with memoization. The memoization ensures that we don’t recompute the same subproblems multiple times. Therefore, the time complexity is significantly reduced to O(n * sqrt(n)), where ‘n’ is the input parameter and sqrt(n) is the maximum number of iterations in the loop. The memo dictionary avoids redundant computations.
• Space complexity: The space complexity is O(n) due to the memoization table. The memo dictionary stores the results of subproblems, and since we memoize for each possible sum from 0 to ‘n’, the space complexity is linear with respect to ‘n’.

  import math
  class Solution:
    def numSquares(self, n: int) -> int:
        memo = defaultdict()
        def dfs(curr_sum):
            if curr_sum == 0:
                return 0
  
            if curr_sum < 0:
                return float('inf')
  
            if curr_sum in memo:
                return memo[curr_sum]
  
            result = float('inf')
            for x in range(1, math.ceil(curr_sum / 2) + 1):
                square = x **2
                result = min(result, dfs(curr_sum - square) + 1)
  
            memo[curr_sum] = result
            return result
  
        return dfs(n)
  

Dynamic Programming - Accepted

Intuition

The dynamic programming approach aims to optimize the solution by iteratively building up the results for each subproblem.

Approach

I initialize a dynamic programming array dp of size (n + 1) with initial values set to ‘n’. The idea is to gradually fill this array with the minimum number of perfect squares required to reach each index.

I then iterate through perfect squares less than or equal to ‘n’, initializing the corresponding indices in the dp array to 1. After that, for each non-perfect square index, I update the dp value by considering all possible perfect squares less than or equal to the current index.

The final result is stored in dp[-1], representing the minimum number of perfect squares required to sum up to ‘n’.

Complexity

• Time complexity: The time complexity is O(n * sqrt(n)), where ‘n’ is the input parameter. The loop iterating through perfect squares up to ‘n’ contributes sqrt(n) iterations, and for each iteration, there’s a nested loop iterating through the closest_square array, which has a maximum length of sqrt(n).

• Space complexity: The space complexity is O(n) due to the dp array, which stores the minimum number of perfect squares required for each subproblem. Additionally, the closest_square array has a maximum length of sqrt(n), contributing to the overall space complexity.

Code

class Solution:
    def numSquares(self, n: int) -> int:
        dp = [n] * (n + 1)
        dp[0] = 0
        x = 1
        while x ** 2 <= n:
            dp[x**2] = 1
            x += 1
        
        closest_square = [1]
        for i in range(1, n + 1):
            if dp[i] == 1:
                closest_square.append(i)
            else:
                for square in closest_square:
                    dp[i] = min(dp[i], dp[i - square] + dp[square])

        return dp[-1]

Editorial Solution

class Solution(object):
    def numSquares(self, n):
        """
        :type n: int
        :rtype: int
        """
        square_nums = [i**2 for i in range(0, int(math.sqrt(n))+1)]
        
        dp = [float('inf')] * (n+1)
        # bottom case
        dp[0] = 0
        
        for i in range(1, n+1):
            for square in square_nums:
                if i < square:
                    break
                dp[i] = min(dp[i], dp[i-square] + 1)
        
        return dp[-1]