Problem of The Day: Count Number of Teams

Problem Statement

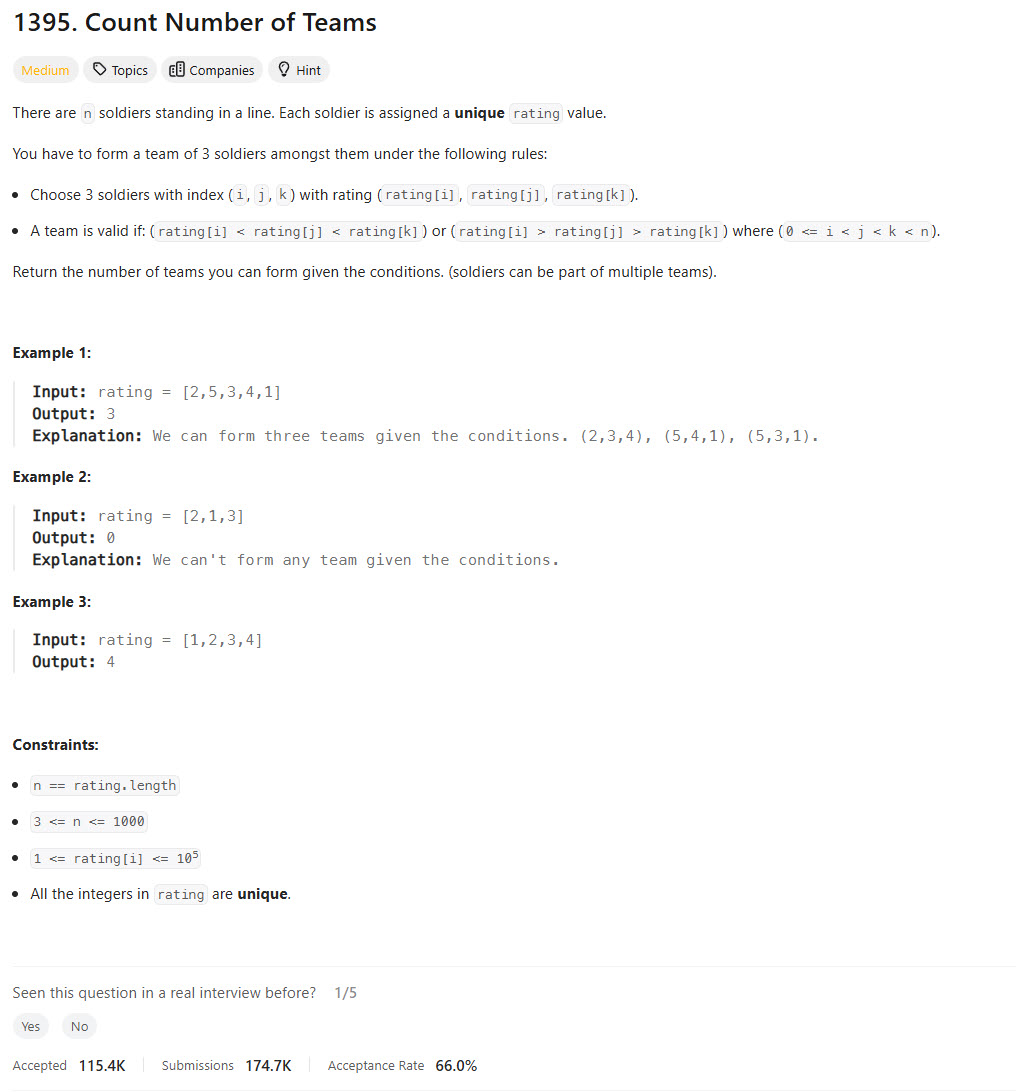
Brute Force - TLE

class Solution:
    def dfs(self, i, curr, rating, visited, desc=False):
        if len(curr) == 3 and curr not in visited:
            visited.append(curr[:])
            return 1
        if i >= len(rating):
            return 0
        res = 0
        for j in range(i, len(rating)):
            if desc:
                if rating[j] < curr[-1]:
                    res += self.dfs(j + 1, curr + [rating[j]], rating, visited, desc=True)
            else:
                if rating[j] > curr[-1]:
                    res += self.dfs(j + 1, curr + [rating[j]], rating, visited)
        return res


    def numTeams(self, rating: List[int]) -> int:
        N = len(rating)
        res = 0
        visited = []
        for i in range(N):
            res += (self.dfs(i, [rating[i]], rating, visited, desc=True) + self.dfs(i, [rating[i]], rating, visited))
        return res

Improved Algorithm

Inspired from the Editorial solution, the idea is to use cache to remove the redundant computation for overlapped sub-solution.

class Solution:
    def dfs(self, i, curr, rating, visited, size, desc=False):
        if size == 3:
            return 1
        if i >= len(rating):
            return 0
        if visited[i][size] != -1:
            return visited[i][size]

        res = 0
        for j in range(i, len(rating)):
            if desc:
                if rating[j] < curr[-1]:
                    res += self.dfs(j + 1, curr + [rating[j]], rating, visited,size + 1, desc=True)
            else:
                if rating[j] > curr[-1]:
                    res += self.dfs(j + 1, curr + [rating[j]], rating, visited, size + 1)
        visited[i][size] = res
        return res


    def numTeams(self, rating: List[int]) -> int:
        N = len(rating)
        res = 0
        asc_cache = [[-1] * 4 for _ in range(N)]
        desc_cache = [[-1] * 4 for _ in range(N)]
        for i in range(N):
            res += (self.dfs(i, [rating[i]], rating, desc_cache, 1, desc=True) + self.dfs(i, [rating[i]], rating, asc_cache, 1))
        return res

Editorial

Approach 1: Dynamic Programming (Memoization)

class Solution:
    def numTeams(self, rating: List[int]) -> int:
        n = len(rating)
        teams = 0
        increasing_cache = [[-1] * 4 for _ in range(n)]
        decreasing_cache = [[-1] * 4 for _ in range(n)]

        # Calculate total teams by considering each soldier as a starting point
        for start_index in range(n):
            teams += self._count_increasing_teams(
                rating, start_index, 1, increasing_cache
            ) + self._count_decreasing_teams(
                rating, start_index, 1, decreasing_cache
            )

        return teams

    def _count_increasing_teams(
        self,
        rating: List[int],
        current_index: int,
        team_size: int,
        increasing_cache: List[List[int]],
    ) -> int:
        n = len(rating)

        # Base case: reached end of array
        if current_index == n:
            return 0

        # Base case: found a valid team of size 3
        if team_size == 3:
            return 1

        # Return cached result if available
        if increasing_cache[current_index][team_size] != -1:
            return increasing_cache[current_index][team_size]

        valid_teams = 0

        # Recursively count teams with increasing ratings
        for next_index in range(current_index + 1, n):
            if rating[next_index] > rating[current_index]:
                valid_teams += self._count_increasing_teams(
                    rating, next_index, team_size + 1, increasing_cache
                )

        # Cache and return the result
        increasing_cache[current_index][team_size] = valid_teams
        return valid_teams

    def _count_decreasing_teams(
        self,
        rating: List[int],
        current_index: int,
        team_size: int,
        decreasing_cache: List[List[int]],
    ) -> int:
        n = len(rating)

        # Base case: reached end of array
        if current_index == n:
            return 0

        # Base case: found a valid team of size 3
        if team_size == 3:
            return 1

        # Return cached result if available
        if decreasing_cache[current_index][team_size] != -1:
            return decreasing_cache[current_index][team_size]

        valid_teams = 0

        # Recursively count teams with decreasing ratings
        for next_index in range(current_index + 1, n):
            if rating[next_index] < rating[current_index]:
                valid_teams += self._count_decreasing_teams(
                    rating, next_index, team_size + 1, decreasing_cache
                )

        # Cache and return the result
        decreasing_cache[current_index][team_size] = valid_teams
        return valid_teams

Approach 2: Dynamic Programming (Tabulation)

class Solution:
    def numTeams(self, rating: List[int]) -> int:
        n = len(rating)
        teams = 0

        # Tables for increasing and decreasing sequences
        increasing_teams = [[0] * 4 for _ in range(n)]
        decreasing_teams = [[0] * 4 for _ in range(n)]

        # Fill the base cases. (Each soldier is a sequence of length 1)
        for i in range(n):
            increasing_teams[i][1] = 1
            decreasing_teams[i][1] = 1

        # Fill the tables
        for count in range(2, 4):
            for i in range(n):
                for j in range(i + 1, n):
                    if rating[j] > rating[i]:
                        increasing_teams[j][count] += increasing_teams[i][
                            count - 1
                        ]
                    if rating[j] < rating[i]:
                        decreasing_teams[j][count] += decreasing_teams[i][
                            count - 1
                        ]

        # Sum up the results (All sequences of length 3)
        for i in range(n):
            teams += increasing_teams[i][3] + decreasing_teams[i][3]

        return teams