Problem of The Day: Water Bottles

Problem Statement

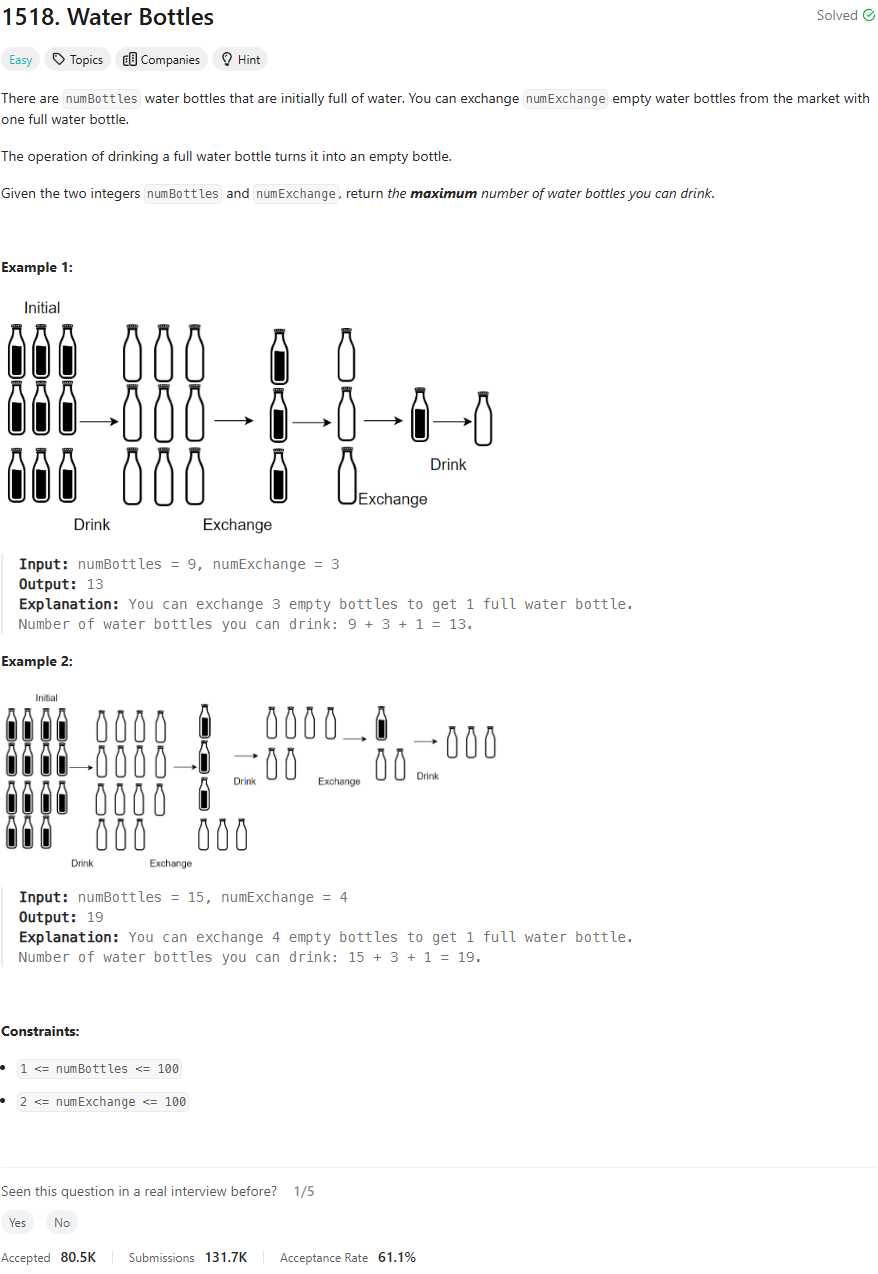
Intuition

My first thought on solving this problem is to simulate the process of drinking and exchanging water bottles. The key is to keep track of the number of full bottles we have, the number of empty bottles we accumulate, and how we can exchange these empty bottles for new full ones. By doing this, I can determine the total number of bottles we can drink.

Approach

1. Initialize res with the initial number of water bottles (numBottles) as we can drink all of these.
2. Use a while loop to continue the process as long as we have enough empty bottles to exchange for at least one full bottle (numBottles >= numExchange).
3. In each iteration:
   • Calculate the remaining empty bottles after the exchange using the modulus operation (emptyBottles = numBottles % numExchange).
   • Determine the number of new full bottles we get from exchanging the empty ones (numBottles = numBottles // numExchange).
   • Add the newly obtained full bottles to the total count (res += numBottles).
   • Update the number of full bottles by adding the remaining empty bottles (numBottles += emptyBottles).
4. Continue this process until we can no longer exchange empty bottles for full ones.
5. Return the total count of water bottles consumed.

Complexity

• Time complexity: The time complexity is \(O(\log_{numExchange}(numBottles))\) because in each iteration, the number of full bottles is reduced by a factor related to numExchange.

• Space complexity: The space complexity is \(O(1)\) as we are using a constant amount of extra space.

Code

class Solution:
    def numWaterBottles(self, numBottles: int, numExchange: int) -> int:
        res = numBottles
        emptyBottles = 0
        while numBottles >= numExchange:
            emptyBottles = numBottles % numExchange
            numBottles = numBottles // numExchange
            res += numBottles
            numBottles += emptyBottles

        return res

Editorial

Approach 1: Simulation

class Solution:
    def numWaterBottles(self, numBottles: int, numExchange: int) -> int:
        consumed_bottles = 0

        while numBottles >= numExchange:
            # Consume numExchange full bottles.
            consumed_bottles += numExchange
            numBottles -= numExchange

            # Exchange them for one full bottle.
            numBottles += 1

        # Consume the remaining numBottles (less than numExchange).
        return consumed_bottles + numBottles

• time: O(n)
• space: O(1)

Approach 2: Optimized Simulation

class Solution:
    def numWaterBottles(self, numBottles: int, numExchange: int) -> int:
        consumed_bottles = 0

        while numBottles >= numExchange:
            # Maximum number of times we can consume numExchange
            # number of bottles using numBottles.
            K = numBottles // numExchange

            consumed_bottles += numExchange * K
            numBottles -= numExchange * K

            numBottles += K

        return consumed_bottles + numBottles

• time: \(O(\log_{numExchange}(numBottles))\), hence O(log N) where N is the number of initial full bottles.
• space: O(1)