Problem of The Day: Dot Product of Two Sparse Vectors

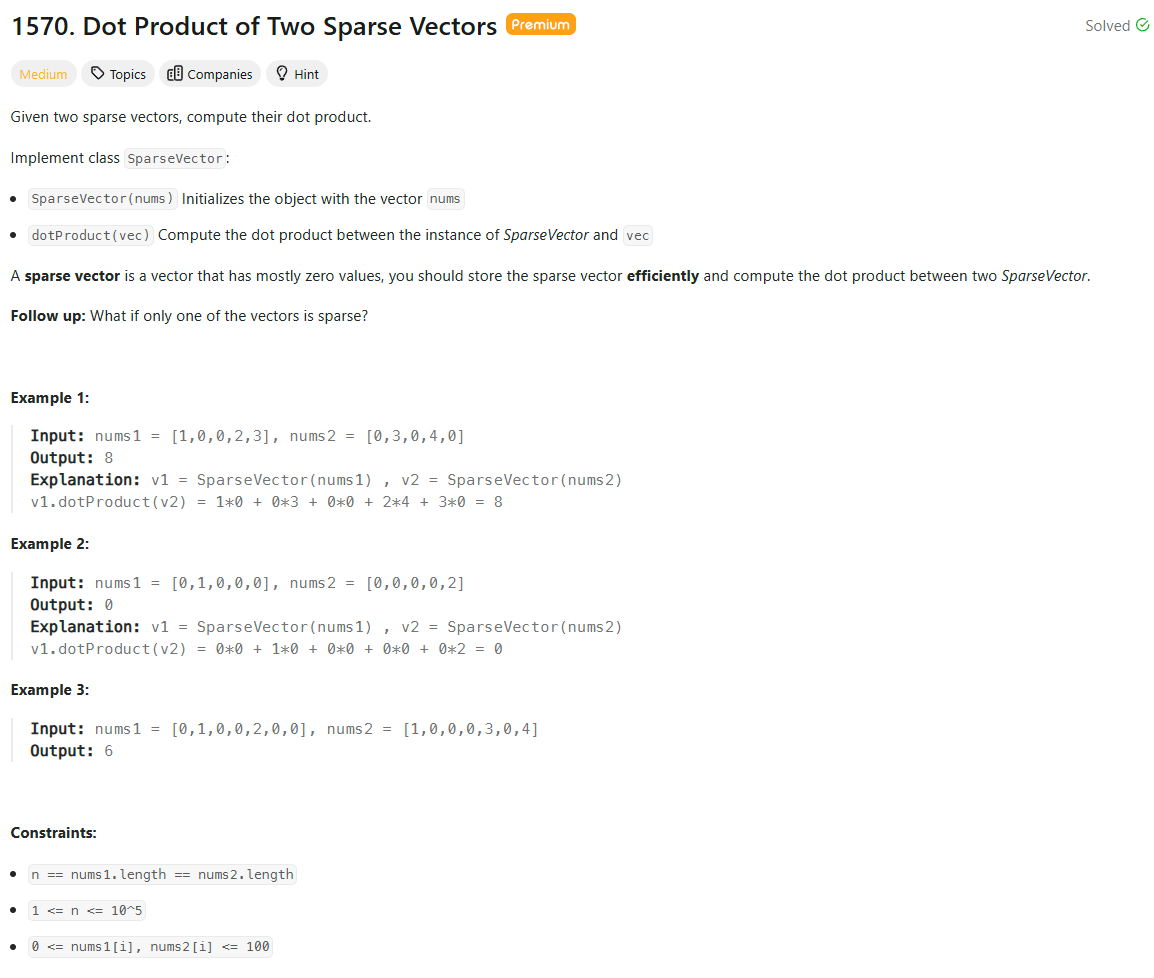
Problem Statement

Intuition

The problem can be optimized by utilizing the sparse nature of the vectors. Sparse vectors have most of their elements as zeros. Instead of iterating through all elements, we can only store and compute non-zero elements to save time.

Approach

1. Store non-zero elements of the vector in a dictionary where the key is the index and the value is the element.
2. To compute the dot product, iterate through the indices of the non-zero elements and multiply corresponding elements from the two vectors if they exist in both.
3. This approach avoids unnecessary computation for zero elements, making the algorithm efficient for sparse data.

Complexity

• Time complexity:
  The time complexity is proportional to the number of non-zero elements in the vectors. If k is the number of non-zero elements, then the time complexity is \(O(k)\).

• Space complexity:
  The space complexity is \(O(k)\) where k is the number of non-zero elements stored in the dictionary.

Code

class SparseVector:
    def __init__(self, nums: List[int]):
        self.vec = {i: nums[i] for i in range(len(nums)) if nums[i] != 0}
        self.len = len(nums)

    # Return the dotProduct of two sparse vectors
    def dotProduct(self, vec: 'SparseVector') -> int:
        res = 0
        for i in range(self.len):
            if i in self.vec and i in vec.vec:
                res += self.vec[i] * vec.vec[i]
        return res

# Your SparseVector object will be instantiated and called as such:
# v1 = SparseVector(nums1)
# v2 = SparseVector(nums2)
# ans = v1.dotProduct(v2)

Editorial

Approach 1: Non-efficient Array Approach

class SparseVector:
    def __init__(self, nums):
        self.array = nums

    def dotProduct(self, vec):
        result = 0
        for num1, num2 in zip(self.array, vec.array):
            result += num1 * num2
        return result

• time: O(n)
• space: O(1)

Approach 2: Hash Table

class SparseVector:
    def __init__(self, nums: List[int]):
        self.nonzeros = {}
        for i, n in enumerate(nums):
            if n != 0:
                self.nonzeros[i] = n

    def dotProduct(self, vec: 'SparseVector') -> int:
        result = 0
        # iterate through each non-zero element in this sparse vector
        # update the dot product if the corresponding index has a non-zero value in the other vector
        for i, n in self.nonzeros.items():
            if i in vec.nonzeros:
                result += n * vec.nonzeros[i]
        return result

• time: O(n)
• space: O(L) for creating hash map, and O(1) for calculating dot product.

Approach 3: Index-Value Pairs

class SparseVector:
    def __init__(self, nums: List[int]):
        self.pairs = []
        for index, value in enumerate(nums):
            if value != 0:
                self.pairs.append([index, value])

    def dotProduct(self, vec: 'SparseVector') -> int:
        result = 0
        p, q = 0, 0

        while p < len(self.pairs) and q < len(vec.pairs):
            if self.pairs[p][0] == vec.pairs[q][0]:
                result += self.pairs[p][1] * vec.pairs[q][1]
                p += 1
                q += 1
            elif self.pairs[p][0] < vec.pairs[q][0]:
                p += 1
            else:
                q += 1

        return result

• time: O(n)
• space: O(L)