Problem of The Day: Maximum XOR for Each Query

Problem Statement

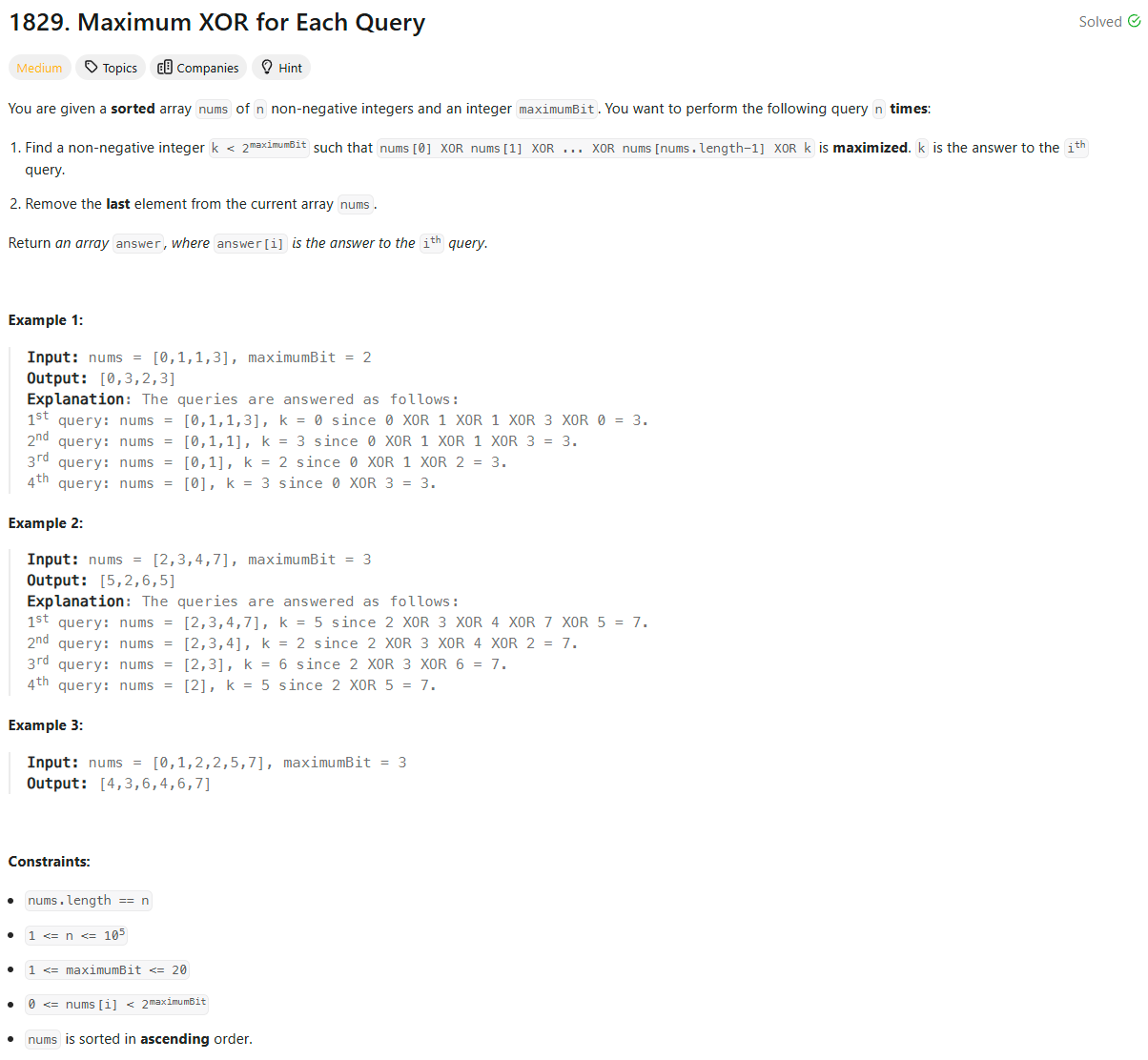
Intuition

The problem requires calculating the maximum XOR for each element in a list of prefix XORs. The idea is to use the XOR operation’s properties to derive each maximum XOR efficiently. Specifically, by targeting the maximum possible value based on maximumBit, we can find the optimal XOR result by using a reverse prefix XOR calculation.

Approach

1. Prefix XOR Calculation:

   • We start by iterating over each element in the input list nums to calculate the prefix XOR. This accumulates the XOR result up to each index and stores it in the prefix array.

2. Target Calculation:

   • To maximize the XOR result, we calculate the largest possible value we can XOR against, which is 2^maximumBit - 1. This ensures all bits up to maximumBit are set to 1.

3. Reverse XOR and Result Construction:

   • For each prefix XOR (starting from the end of the list), we XOR it with the target to get the desired maximum XOR value.
   • We store each result in res, building it in reverse order.

Complexity

• Time complexity:
  The algorithm iterates over nums twice (once to calculate the prefix XORs and once to build the result list), making the time complexity \(O(N)\) where N is the length of nums.

• Space complexity:
  The algorithm uses two additional lists of size N, one for storing the prefix XORs and one for the results. Thus, the space complexity is \(O(N)\).

Code

class Solution:
    def getMaximumXor(self, nums: List[int], maximumBit: int) -> List[int]:
        N = len(nums)
        curr = 0
        prefix = [0] * N
        for i, num in enumerate(nums):
            curr = curr ^ num
            prefix[i] = curr

        res = [0] * N
        target = 2**maximumBit - 1
        for i in range(N):
            k = prefix[N - i - 1] ^ target
            res[i] = k
        return res

Editorial

Approach 1: Prefix Array + Bit Masking

class Solution:
    def getMaximumXor(self, nums: List[int], maximumBit: int) -> List[int]:
        prefix_xor = [0] * len(nums)
        prefix_xor[0] = nums[0]
        for i in range(1, len(nums)):
            prefix_xor[i] = prefix_xor[i - 1] ^ nums[i]
        ans = [0] * len(nums)

        mask = (1 << maximumBit) - 1

        for i in range(len(nums)):
            # find k to maximize value
            current_xor = prefix_xor[len(prefix_xor) - 1 - i]
            ans[i] = current_xor ^ mask

        return ans

• time: O(n)
• space: O(n)

Approach 2: Optimized Calculation + Bit Masking

class Solution:
    def getMaximumXor(self, nums: List[int], maximumBit: int) -> List[int]:
        xor_product = 0
        for i in range(len(nums)):
            xor_product = xor_product ^ nums[i]
        ans = [0] * len(nums)

        mask = (1 << maximumBit) - 1

        for i in range(len(nums)):
            ans[i] = xor_product ^ mask
            # remove last element
            xor_product = xor_product ^ nums[len(nums) - 1 - i]

        return ans

• time: O(n)
• space: O(1)