Problem of The Day: Count Sub Islands
Problem Statement
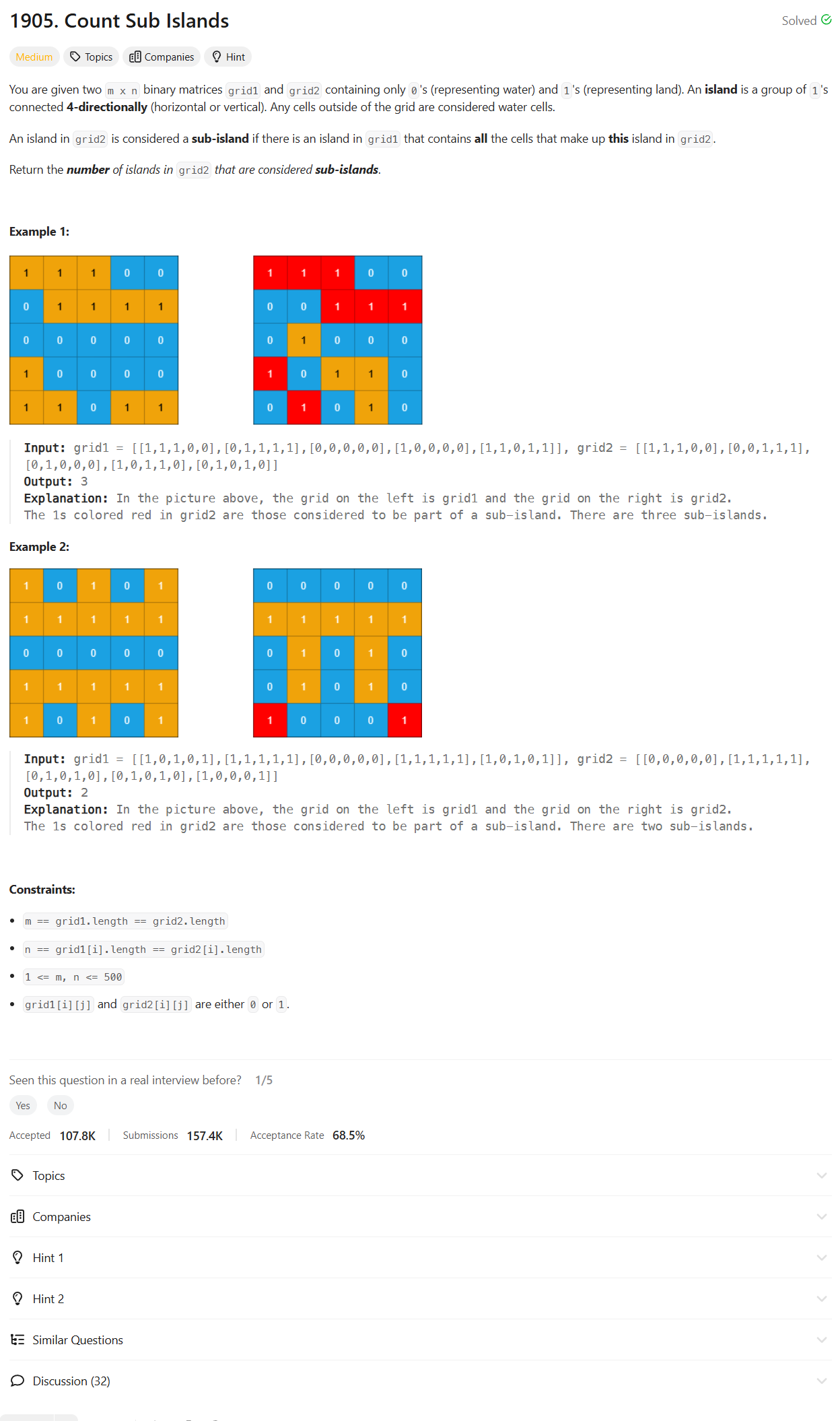
Intuition
When I first encountered this problem, I realized that I needed to determine if an island in the second grid is fully contained within an island in the first grid. My initial thought was to explore each island in the second grid and check its corresponding area in the first grid.
Approach
My approach was to use a Breadth-First Search (BFS) to explore each island in the second grid. For each island, I marked the visited cells to avoid redundant work. As I explored an island in grid2, I checked if every cell in this island corresponded to a land cell in grid1. If even one cell in grid2 corresponded to a water cell in grid1, I disregarded that island. If all cells matched, I counted it as a valid sub-island.
Complexity
-
Time complexity: The time complexity is \(O(n \times m)\), where
nis the number of rows andmis the number of columns in the grid. This is because in the worst case, we might need to visit every cell ingrid2. -
Space complexity: The space complexity is also \(O(n \times m)\) due to the space needed for the BFS queue, which in the worst case could store all cells.
Code
class Solution:
def countSubIslands(self, grid1: List[List[int]], grid2: List[List[int]]) -> int:
ROWS = len(grid1)
COLS = len(grid1[0])
sub_islands = 0
direction = [(0,1),(-1,0),(0,-1),(1,0)]
def bfs(r, c, grid_1, grid_2):
queue = deque([[r,c]])
other_queue = deque([[r,c]])
grid_2[r][c] = 2
while queue:
curr_row, curr_col = queue.popleft()
other_queue.append([curr_row, curr_col])
for x, y in direction:
next_row, next_col = curr_row + x, curr_col + y
if 0 <= next_row < ROWS and 0 <= next_col < COLS and grid_2[next_row][next_col] == 1:
queue.append([next_row, next_col])
grid_2[next_row][next_col] = 2
while other_queue:
row, col = other_queue.popleft()
if grid_1[row][col] != 1:
return 0
return 1
for row in range(ROWS):
for col in range(COLS):
if grid2[row][col] == 1 and grid1[row][col] == 1:
sub_islands += bfs(row, col, grid1, grid2)
return sub_islands
Editorial Solution
Approach 1: Breadth-First Search (BFS)
class Solution:
# Directions in which we can traverse inside the grids.
directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
# Helper method to check if the cell at the position (x, y) in the 'grid'
# is a land cell.
def is_cell_land(self, x, y, grid):
return grid[x][y] == 1
# Traverse all cells of island starting at position (x, y) in 'grid2',
# and check this island is a sub-island in 'grid1'.
def is_sub_island(self, x, y, grid1, grid2, visited):
total_rows = len(grid2)
total_cols = len(grid2[0])
is_sub_island = True
pending_cells = deque()
# Push the starting cell in the queue and mark it as visited.
pending_cells.append((x, y))
visited[x][y] = True
# Traverse on all cells using the breadth-first search method.
while pending_cells:
curr_x, curr_y = pending_cells.popleft()
# If the current position cell is not a land cell in 'grid1',
# then the current island can't be a sub-island.
if not self.is_cell_land(curr_x, curr_y, grid1):
is_sub_island = False
for direction in self.directions:
next_x = curr_x + direction[0]
next_y = curr_y + direction[1]
# If the next cell is inside 'grid2', is never visited and
# is a land cell, then we traverse to the next cell.
if (
0 <= next_x < total_rows
and 0 <= next_y < total_cols
and not visited[next_x][next_y]
and self.is_cell_land(next_x, next_y, grid2)
):
# Push the next cell in the queue and mark it as visited.
pending_cells.append((next_x, next_y))
visited[next_x][next_y] = True
return is_sub_island
def countSubIslands(
self, grid1: List[List[int]], grid2: List[List[int]]
) -> int:
total_rows = len(grid2)
total_cols = len(grid2[0])
visited = [[False] * total_cols for _ in range(total_rows)]
sub_island_counts = 0
# Iterate on each cell in 'grid2'
for x in range(total_rows):
for y in range(total_cols):
# If cell at the position (x, y) in the 'grid2' is not visited,
# is a land cell in 'grid2', and the island
# starting from this cell is a sub-island in 'grid1', then we
# increment the count of sub-islands.
if (
not visited[x][y]
and self.is_cell_land(x, y, grid2)
and self.is_sub_island(x, y, grid1, grid2, visited)
):
sub_island_counts += 1
# Return total count of sub-islands.
return sub_island_counts
Approach 2: Depth-First Search
class Solution:
# Directions in which we can traverse inside the grids.
directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
# Helper method to check if the cell at the position (x, y) in the 'grid'
# is a land cell.
def is_cell_land(self, x, y, grid):
return grid[x][y] == 1
# Traverse all cells of island starting at position (x, y) in 'grid2',
# and check if this island is a sub-island in 'grid1'.
def is_sub_island(self, x, y, grid1, grid2, visited):
total_rows = len(grid2)
total_cols = len(grid2[0])
# Traverse on all cells using the depth-first search method.
is_sub_island = True
# If the current cell is not a land cell in 'grid1', then the current island can't be a sub-island.
if not self.is_cell_land(x, y, grid1):
is_sub_island = False
# Traverse on all adjacent cells.
for direction in self.directions:
next_x = x + direction[0]
next_y = y + direction[1]
# If the next cell is inside 'grid2', is not visited, and is a land cell,
# then we traverse to the next cell.
if (
0 <= next_x < total_rows
and 0 <= next_y < total_cols
and not visited[next_x][next_y]
and self.is_cell_land(next_x, next_y, grid2)
):
# Mark the next cell as visited.
visited[next_x][next_y] = True
next_cell_is_part_of_sub_island = self.is_sub_island(
next_x, next_y, grid1, grid2, visited
)
is_sub_island = (
is_sub_island and next_cell_is_part_of_sub_island
)
return is_sub_island
def countSubIslands(
self, grid1: List[List[int]], grid2: List[List[int]]
) -> int:
total_rows = len(grid2)
total_cols = len(grid2[0])
visited = [[False] * total_cols for _ in range(total_rows)]
sub_island_counts = 0
# Iterate over each cell in 'grid2'.
for x in range(total_rows):
for y in range(total_cols):
# If the cell at position (x, y) in 'grid2' is not visited,
# is a land cell in 'grid2', and the island starting from this cell is a sub-island in 'grid1',
# then increment the count of sub-islands.
if not visited[x][y] and self.is_cell_land(x, y, grid2):
visited[x][y] = True
if self.is_sub_island(x, y, grid1, grid2, visited):
sub_island_counts += 1
# Return total count of sub-islands.
return sub_island_counts
Approach 3: Union-Find
class Solution:
# Directions in which we can traverse inside the grids.
directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
# Helper method to check if the cell at the position (x, y) in the 'grid'
# is a land cell.
def is_cell_land(self, x, y, grid):
return grid[x][y] == 1
# Union-Find class.
class UnionFind:
def __init__(self, n):
self.parent = list(range(n))
self.rank = [0] * n
# Find the root of element 'u', using the path-compression technique.
def find(self, u):
if self.parent[u] != u:
self.parent[u] = self.find(self.parent[u])
return self.parent[u]
# Union two components of elements 'u' and 'v' respectively based on their ranks.
def union_sets(self, u, v):
root_u = self.find(u)
root_v = self.find(v)
if root_u != root_v:
if self.rank[root_u] > self.rank[root_v]:
self.parent[root_v] = root_u
elif self.rank[root_u] < self.rank[root_v]:
self.parent[root_u] = root_v
else:
self.parent[root_v] = root_u
self.rank[root_u] += 1
# Helper method to convert (x, y) position to a 1-dimensional index.
def convert_to_index(self, x, y, total_cols):
return x * total_cols + y
def countSubIslands(
self, grid1: List[List[int]], grid2: List[List[int]]
) -> int:
total_rows = len(grid2)
total_cols = len(grid2[0])
uf = self.UnionFind(total_rows * total_cols)
# Traverse each land cell of 'grid2'.
for x in range(total_rows):
for y in range(total_cols):
if self.is_cell_land(x, y, grid2):
# Union adjacent land cells with the current land cell.
for direction in self.directions:
next_x = x + direction[0]
next_y = y + direction[1]
if (
0 <= next_x < total_rows
and 0 <= next_y < total_cols
and self.is_cell_land(next_x, next_y, grid2)
):
uf.union_sets(
self.convert_to_index(x, y, total_cols),
self.convert_to_index(
next_x, next_y, total_cols
),
)
# Traverse 'grid2' land cells and mark that cell's root as not a sub-island
# if the land cell is not present at the respective position in 'grid1'.
is_sub_island = [True] * (total_rows * total_cols)
for x in range(total_rows):
for y in range(total_cols):
if self.is_cell_land(x, y, grid2) and not self.is_cell_land(
x, y, grid1
):
root = uf.find(self.convert_to_index(x, y, total_cols))
is_sub_island[root] = False
# Count all the sub-islands.
sub_island_counts = 0
for x in range(total_rows):
for y in range(total_cols):
if self.is_cell_land(x, y, grid2):
root = uf.find(self.convert_to_index(x, y, total_cols))
if is_sub_island[root]:
sub_island_counts += 1
# One cell can be the root of multiple land cells, so to
# avoid counting the same island multiple times, mark it as false.
is_sub_island[root] = False
return sub_island_counts