Problem of The Day: Path with Maximum Probability

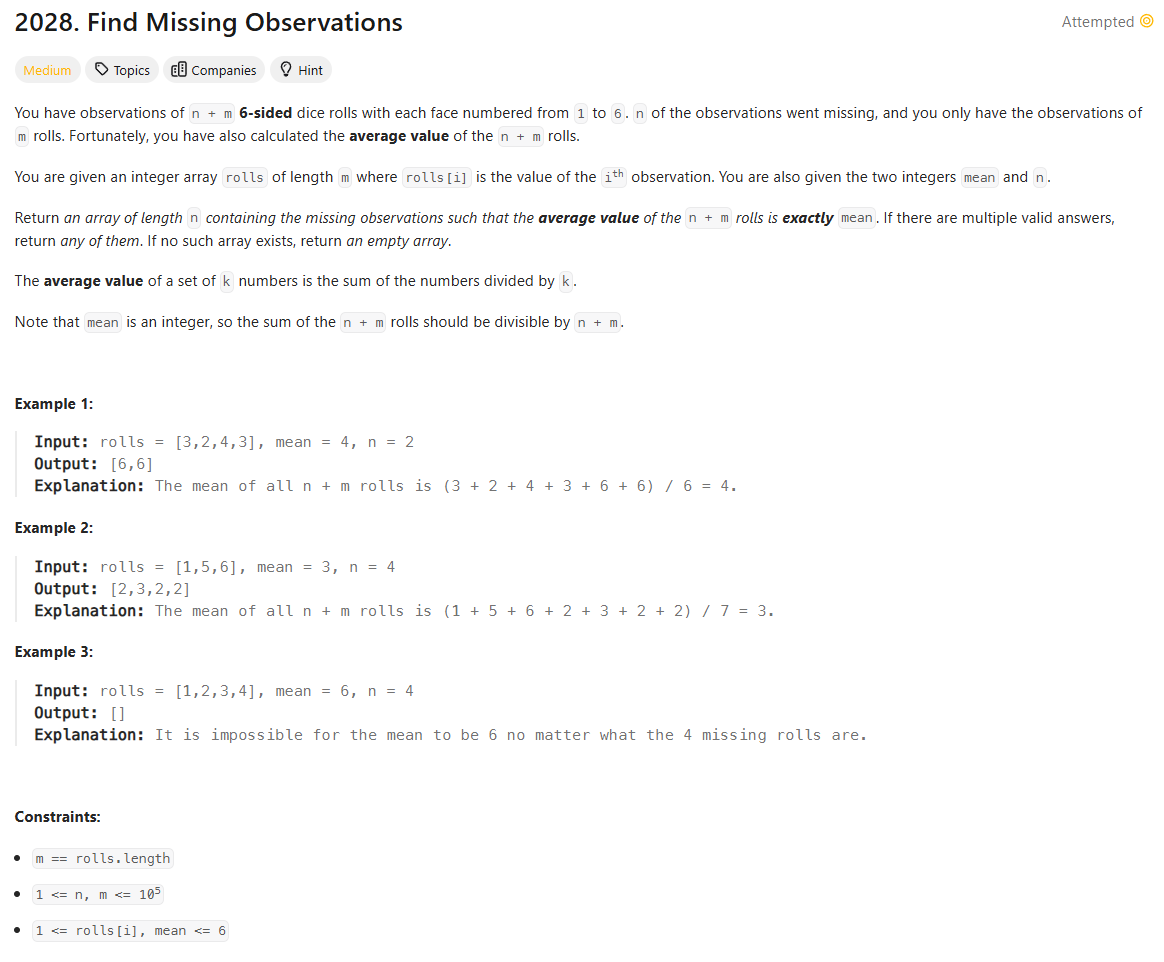
Problem Statement

Brute Force - TLE

class Solution:
    def dfs(self, i, target, n, curr):
        if target == 0:
            return [True, curr]
        if len(curr) >= n or target < 0:
            return [False, []]
        for j in range(i, 7):
            ans, res = self.dfs(j, target - j, n, curr + [j])
            if ans:
                return [ans, res]
            ans, res = self.dfs(j + 1, target - j, n, curr + [j])
            if ans:
                return [ans, res]
        return [False, []]


    def missingRolls(self, rolls: List[int], mean: int, n: int) -> List[int]:
        m = len(rolls)
        total_sum = (m + n) * mean
        missing_sum = total_sum - sum(rolls)
        return self.dfs(1, missing_sum, n, [])[1]

Editorial

class Solution:
    def missingRolls(self, rolls: List[int], mean: int, n: int) -> List[int]:
        sum_rolls = sum(rolls)
        # Find the remaining sum.
        remaining_sum = mean * (n + len(rolls)) - sum_rolls
        # Check if sum is valid or not.
        if remaining_sum > 6 * n or remaining_sum < n:
            return []
        distribute_mean = remaining_sum // n
        mod = remaining_sum % n
        # Distribute the remaining mod elements in n_elements list.
        n_elements = [distribute_mean] * n
        for i in range(mod):
            n_elements[i] += 1
        return n_elements

• time: O(max(m*n))
• space: O(1)