Thomas Ngo

Software Engineer

3 minute read

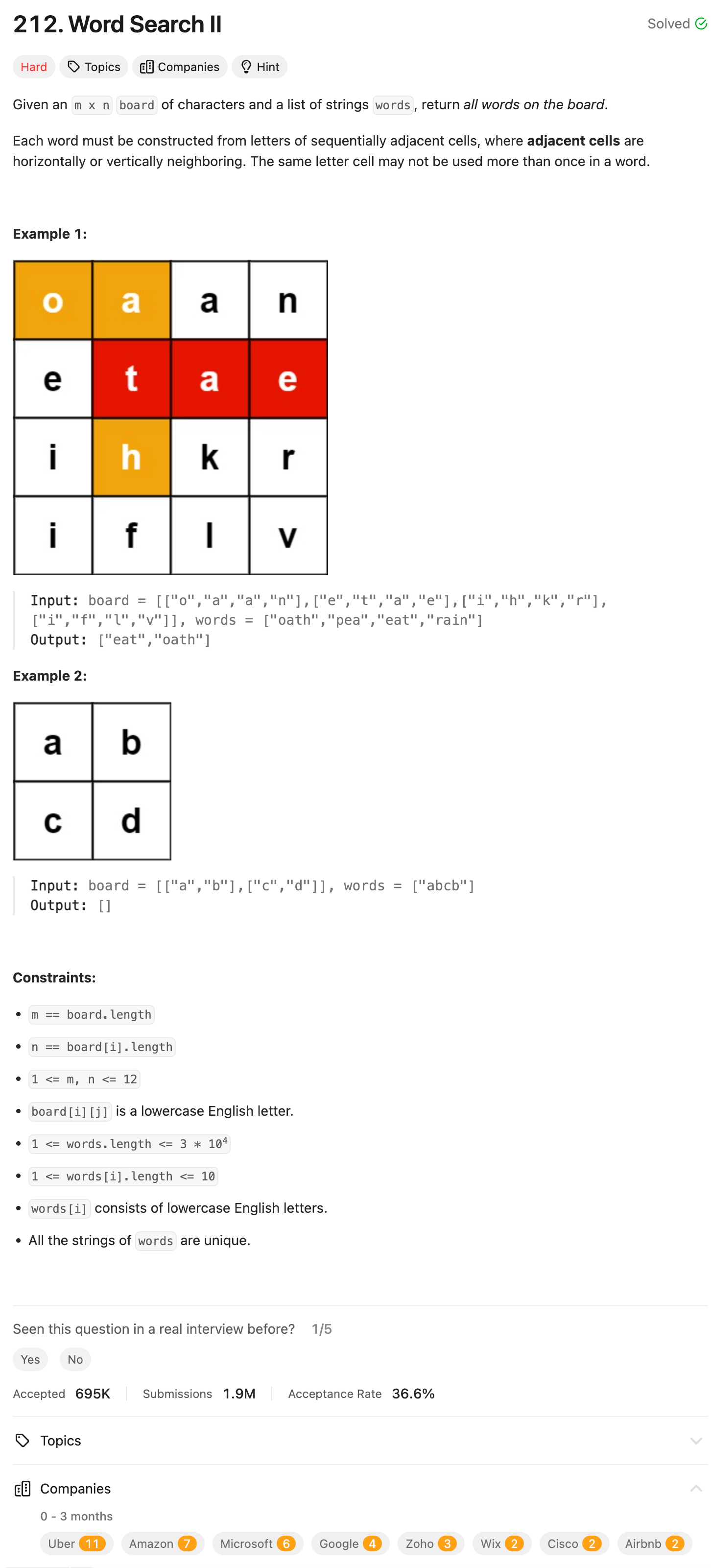
Problem Statement

problem

Intuition

We can efficiently solve this problem by building a Trie from the list of words and using a backtracking algorithm to search the 2D board. The Trie allows us to quickly determine if the current character on the board can form part of a word in the dictionary. The backtracking ensures that we explore all potential words that can be formed by connecting adjacent characters.

Approach

  1. Construct a Trie from the list of words to efficiently check if a word or prefix exists.
  2. For each character in the board, use a backtracking algorithm to explore all possible paths, checking if they form a valid word.
  3. During backtracking, mark the board position as visited by temporarily replacing the character with a special symbol (e.g., ##) to avoid revisiting it.
  4. If a word is found during the search, add it to the result list.
  5. After exploring, reset the visited character to its original state.

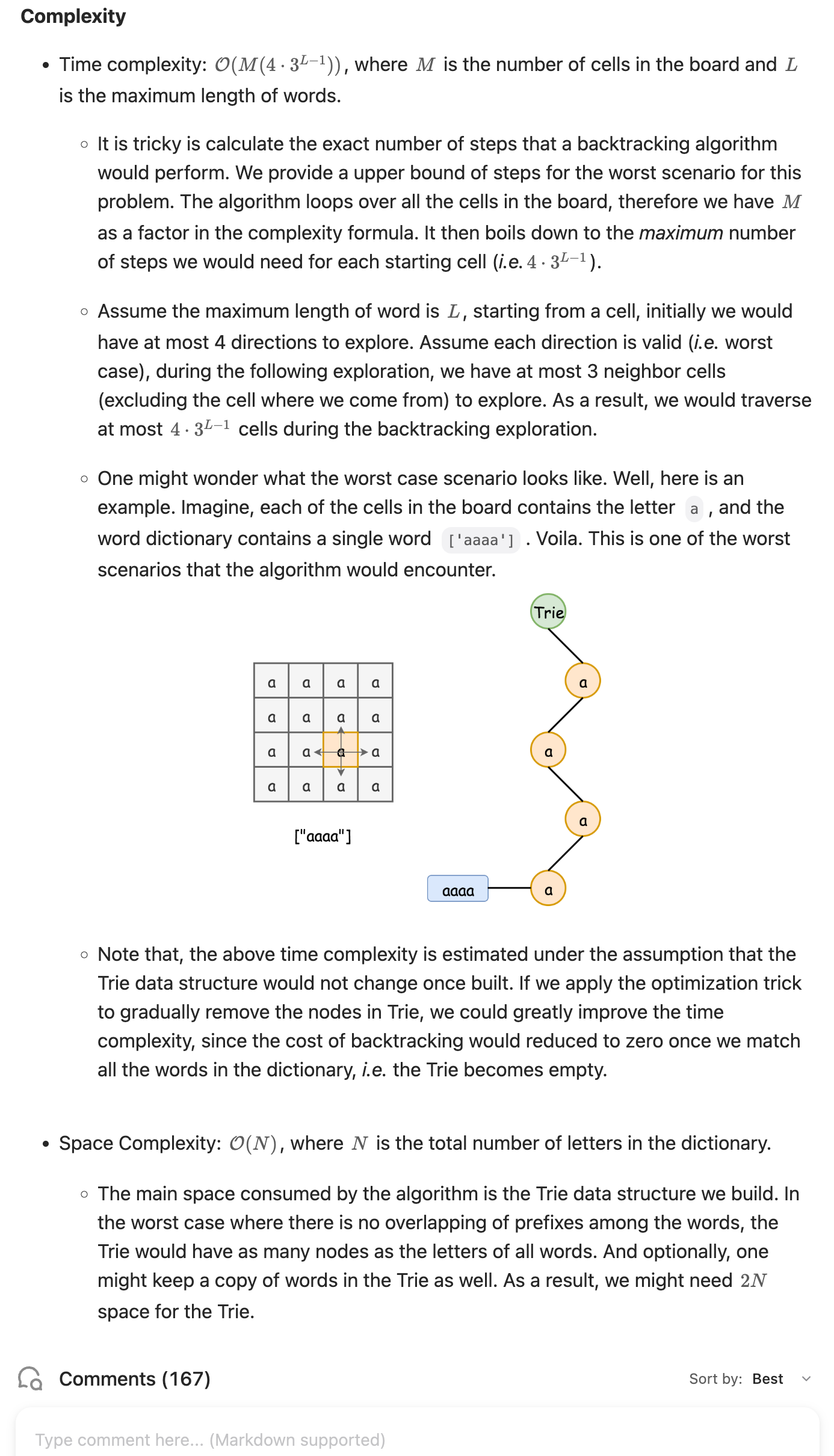
Complexity

  • Time complexity: The time complexity is \(O(m \cdot n \cdot 4^l)\), where \(m \cdot n\) represents the size of the board, and \(l\) is the maximum length of the word in the dictionary. In the worst case, we may need to explore all four directions for each cell, leading to the factor of \(4^l\) for backtracking.

  • Space complexity: The space complexity is \(O(l)\) due to the recursion depth during backtracking, where \(l\) is the length of the longest word. Additionally, building the Trie takes \(O(W \cdot L)\), where \(W\) is the number of words and \(L\) is the average length of the words.

Code

class Solution:
    def backtrack(self, row, col, board, res, trie):
        ROWS = len(board)
        COLS = len(board[0])
        if '#' in trie and trie['#'] not in res:
            res.append(trie['#'])

        temp = board[row][col]
        board[row][col] = '#'
        for x, y in [(1,0),(0,1),(-1,0),(0,-1)]:
            r, c = row + x, col + y
            if 0 <= r < ROWS and 0 <= c < COLS and board[r][c] in trie:
                self.backtrack(r, c, board, res, trie[board[r][c]])
        board[row][col] = temp

    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
        trie = {}
        ROWS = len(board)
        COLS = len(board[0])
        res = []
        for word in words:
            root = trie
            for c in word:
                if c not in root:
                    root[c] = {}
                root = root[c]
            root['#'] = word
        for row in range(ROWS):
            for col in range(COLS):
                if board[row][col] in trie:
                    self.backtrack(row, col, board, res, trie[board[row][col]])

        return res

Editorial

Approach 1: Backtracking with Trie

class Solution:
    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
        WORD_KEY = "$"

        trie = {}
        for word in words:
            node = trie
            for letter in word:
                # retrieve the next node; If not found, create a empty node.
                node = node.setdefault(letter, {})
            # mark the existence of a word in trie node
            node[WORD_KEY] = word

        rowNum = len(board)
        colNum = len(board[0])

        matchedWords = []

        def backtracking(row, col, parent):

            letter = board[row][col]
            currNode = parent[letter]

            # check if we find a match of word
            word_match = currNode.pop(WORD_KEY, False)
            if word_match:
                # also we removed the matched word to avoid duplicates,
                #   as well as avoiding using set() for results.
                matchedWords.append(word_match)

            # Before the EXPLORATION, mark the cell as visited
            board[row][col] = "#"

            # Explore the neighbors in 4 directions, i.e. up, right, down, left
            for rowOffset, colOffset in [(-1, 0), (0, 1), (1, 0), (0, -1)]:
                newRow, newCol = row + rowOffset, col + colOffset
                if (
                    newRow < 0
                    or newRow >= rowNum
                    or newCol < 0
                    or newCol >= colNum
                ):
                    continue
                if not board[newRow][newCol] in currNode:
                    continue
                backtracking(newRow, newCol, currNode)

            # End of EXPLORATION, we restore the cell
            board[row][col] = letter

            # Optimization: incrementally remove the matched leaf node in Trie.
            if not currNode:
                parent.pop(letter)

        for row in range(rowNum):
            for col in range(colNum):
                # starting from each of the cells
                if board[row][col] in trie:
                    backtracking(row, col, trie)

        return matchedWords

complexity

You may also enjoy