Problem of The Day: Basic Calculator II

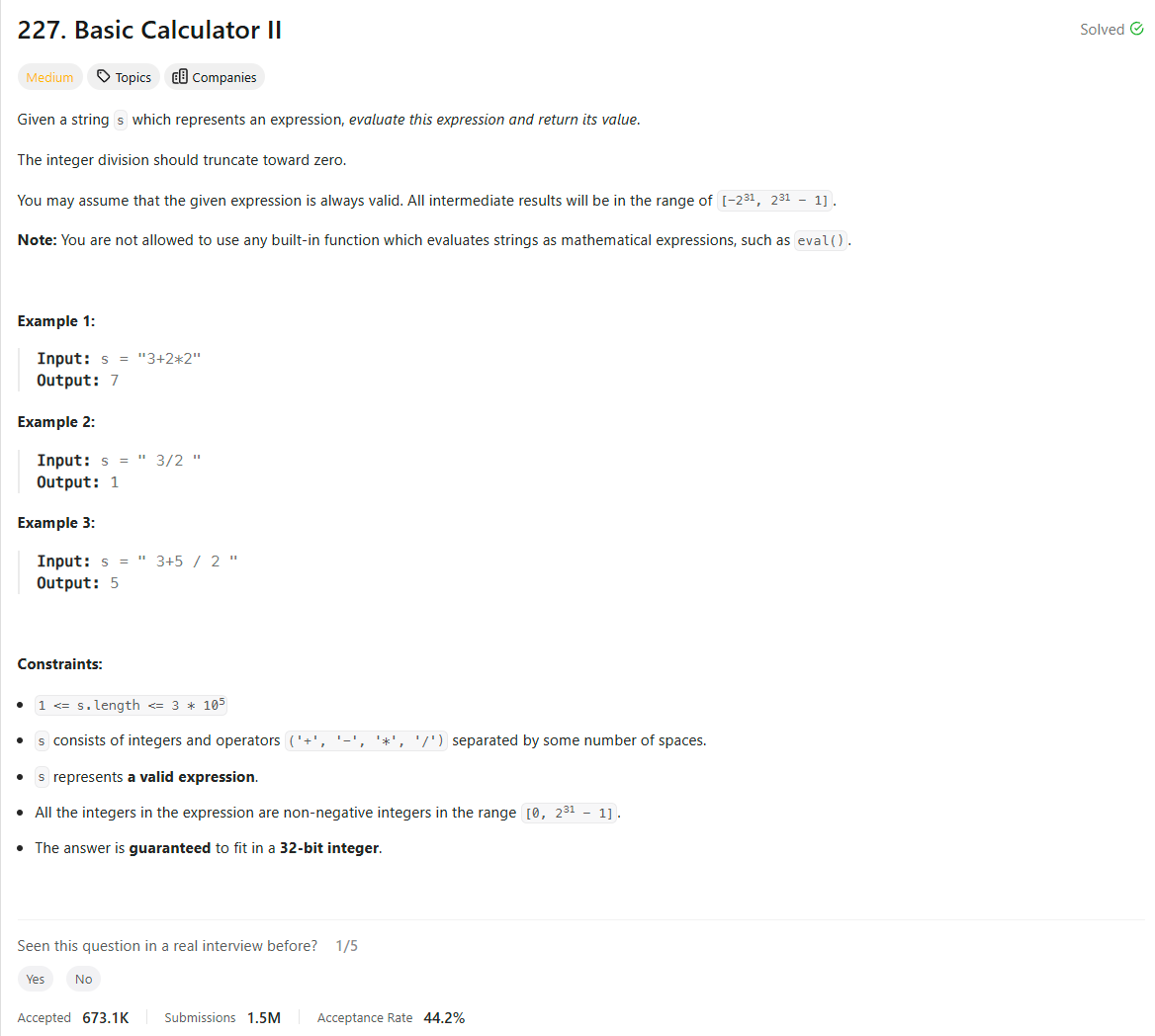
Problem Statement

Intuition

The problem requires evaluating a mathematical expression containing basic arithmetic operations such as addition, subtraction, multiplication, and division. Initially, I thought about using a stack or queue to process the expression step by step and handle operator precedence. Specifically, multiplication and division should be evaluated first before addition and subtraction.

Approach

1. First, I clean up the input string by removing spaces to make parsing easier.
2. I iterate through the string to separate out numbers and operators. Each number and operator is pushed into a queue to maintain the order.
3. In the first pass, I process all multiplication and division operations since they have higher precedence. For each of these operations, I remove the operands from the queue, perform the calculation, and push the result back.
4. In the second pass, I process the remaining addition and subtraction in the same way.
5. The final value left in the queue is the result of the entire expression.

Complexity

• Time complexity: The time complexity is \(O(n)\) because we iterate over the string twice, once for parsing the string and once for evaluating the operations.

• Space complexity: The space complexity is \(O(n)\) as we store the parsed tokens (numbers and operators) in a queue.

Code

from collections import deque

class Solution:
    def calculate(self, s: str) -> int:
        s = s.replace(" ", "")
        calc_expr = {
            '+': lambda x, y: x + y,
            '-': lambda x, y: x - y,
            '*': lambda x, y: x * y,
            '/': lambda x, y: x // y,
        }
        queue = deque()
        start = end = 0
        for end in range(len(s)):
            if s[end] in ('+', '-', '*', '/'):
                queue.append(s[start:end])
                queue.append(s[end])
                start = end + 1
        queue.append(s[start:end+1])

        next_queue = deque()
        while queue:
            ch = queue.popleft()
            if ch in ('*', '/'):
                x = int(next_queue.pop())
                y = int(queue.popleft())
                val = calc_expr[ch](x, y)
                next_queue.append(str(val))
            else:
                next_queue.append(ch)

        while len(next_queue) > 1:
            x = int(next_queue.popleft())
            op = next_queue.popleft()
            y = int(next_queue.popleft())
            val = calc_expr[op](x, y)
            next_queue.appendleft(str(val))

        return int(next_queue[0])

Editorial

Approach 1: Using Stack

class Solution {
public:
    int calculate(string s) {
        int len = s.length();
        if (len == 0) return 0;
        stack<int> stack;
        int currentNumber = 0;
        char operation = '+';
        for (int i = 0; i < len; i++) {
            char currentChar = s[i];
            if (isdigit(currentChar)) {
                currentNumber = (currentNumber * 10) + (currentChar - '0');
            }
            if (!isdigit(currentChar) && !iswspace(currentChar) || i == len - 1) {
                if (operation == '-') {
                    stack.push(-currentNumber);
                } else if (operation == '+') {
                    stack.push(currentNumber);
                } else if (operation == '*') {
                    int stackTop = stack.top();
                    stack.pop();
                    stack.push(stackTop * currentNumber);
                } else if (operation == '/') {
                    int stackTop = stack.top();
                    stack.pop();
                    stack.push(stackTop / currentNumber);
                }
                operation = currentChar;
                currentNumber = 0;
            }
        }
        int result = 0;
        while (stack.size() != 0) {
            result += stack.top();
            stack.pop();
        }
        return result;
    }
};

• time: O(n)
• space: O(n)

Approach 2: Optimised Approach without the stack

class Solution {
public:
    int calculate(string s) {
        int length = s.length();
        if (length == 0) return 0;
        int currentNumber = 0, lastNumber = 0, result = 0;
        char sign = '+';
        for (int i = 0; i < length; i++) {
            char currentChar = s[i];
            if (isdigit(currentChar)) {
                currentNumber = (currentNumber * 10) + (currentChar - '0');
            }
            if (!isdigit(currentChar) && !iswspace(currentChar) || i == length - 1) {
                if (sign == '+' || sign == '-') {
                    result += lastNumber;
                    lastNumber = (sign == '+') ? currentNumber : -currentNumber;
                } else if (sign == '*') {
                    lastNumber = lastNumber * currentNumber;
                } else if (sign == '/') {
                    lastNumber = lastNumber / currentNumber;
                }
                sign = currentChar;
                currentNumber = 0;
            }
        }
        result += lastNumber;
        return result;
    }
};