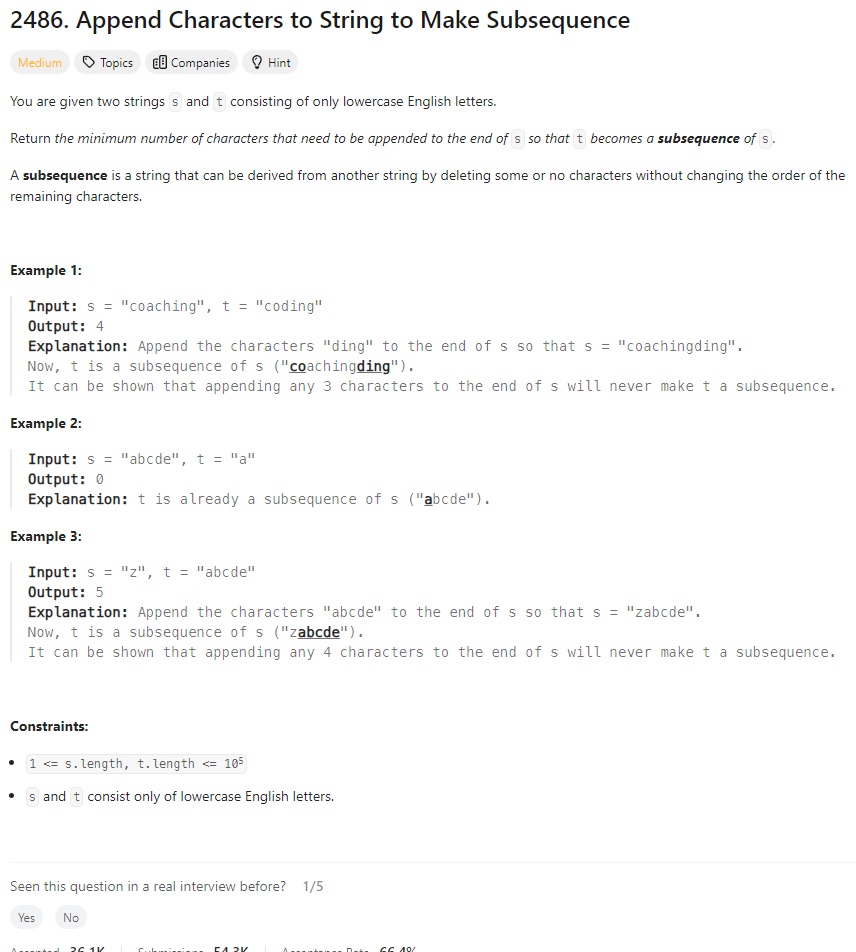
Problem of The Day: Append Characters to String to Make Subsequence

Problem Statement

Brute Force - TLE

class Solution:
    def appendCharacters(self, s: str, t: str) -> int:
        res = float('inf')
        s_len = len(s)
        t_len = len(t)
        for i in range(s_len):
            for j in range(i, s_len):
                l = j
                k = 0
                if s[l] == t[k]:
                    while k < t_len and l < s_len:
                        if s[l] == t[k]:
                            k += 1
                        l += 1

                res = min(res, t_len - k)

        return res if res != float('inf') else 0

• Time: O(s_len x s_len x t_len)
• Space: O(s_len ^ 2 x t_len)

Intuition

When I first looked at this problem, I thought about how I can find the minimum number of characters I need to append to the string s to make t a subsequence of s. The goal is to efficiently traverse both strings and determine the necessary number of additional characters.

Approach

My approach involves a two-pointer technique. I use one pointer to traverse s and another pointer to traverse t. I increment both pointers when the characters at their current positions match. If the characters don’t match, I only increment the pointer for s. This way, I effectively find how much of t can be matched by s without any additions. The difference between the length of t and the number of characters matched gives the result.

Complexity

• Time complexity: The time complexity of my approach is (O(n + m)), where (n) is the length of s and (m) is the length of t. This is because we traverse each string at most once.
• Space complexity: The space complexity of my approach is (O(1)) because I only use a fixed amount of extra space for the pointers and a few variables.

Code

class Solution:
    def appendCharacters(self, s: str, t: str) -> int:
        s_len = len(s)
        t_len = len(t)
        s_idx, t_idx = 0, 0
        while s_idx < s_len and t_idx < t_len:
            if s[s_idx] == t[t_idx]:
                t_idx += 1
            s_idx += 1

        return t_len - t_idx

Editorial

class Solution:
    def appendCharacters(self, s: str, t: str) -> int:
        first = 0
        longest_prefix = 0

        while first < len(s) and longest_prefix < len(t):
            if s[first] == t[longest_prefix]:
                # Since at the current position both the characters are equal,
                # increment longest_prefix by 1
                longest_prefix += 1
            first += 1

        # The number of characters appended is given by the difference in length of t
        # and longest_prefix
        return len(t) - longest_prefix

• Time: O(n)
• Space: O(1)