Thomas Ngo

Software Engineer

3 minute read

Problem Statement

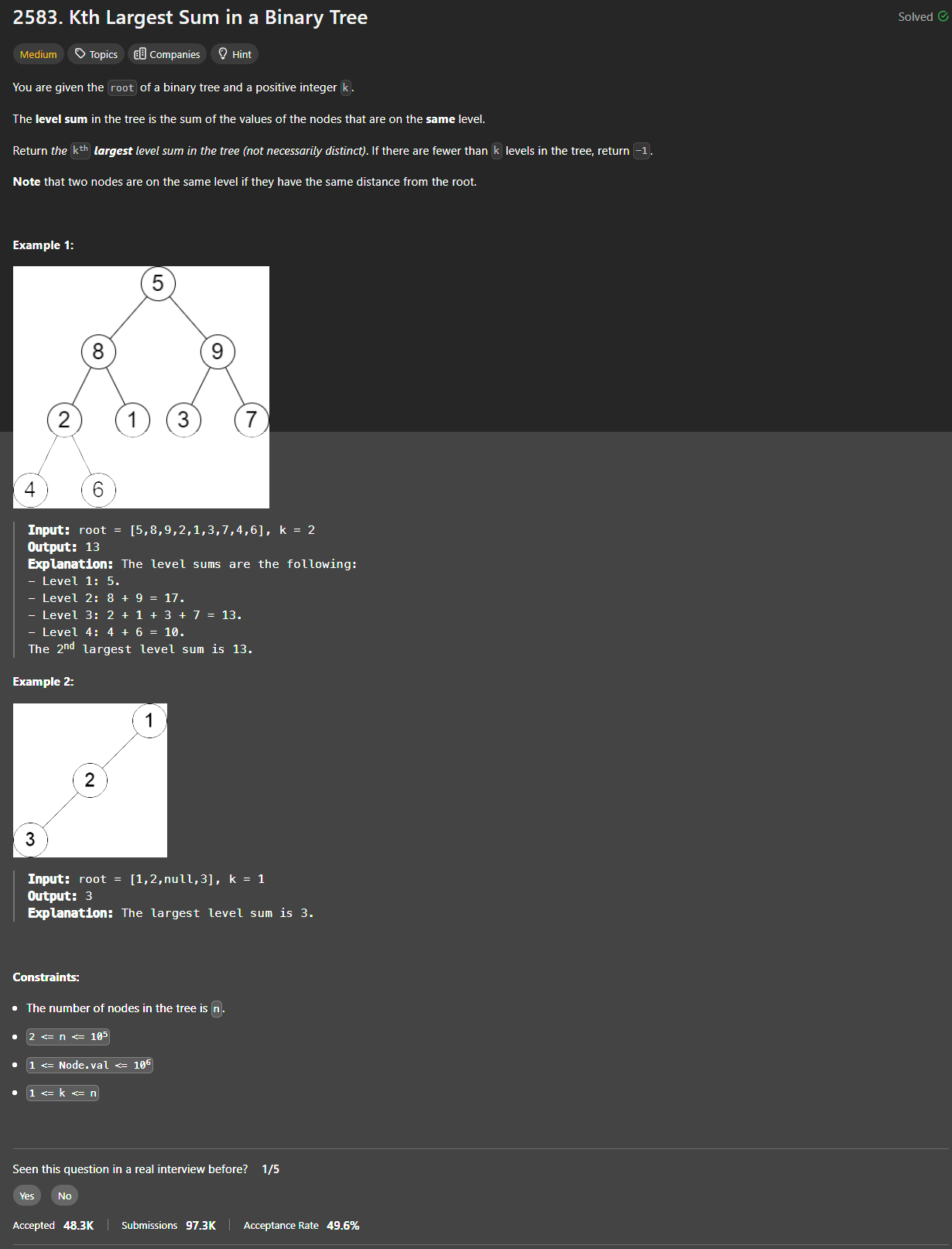
problem

Intuition

When I first encountered this problem, my initial thought was that it would require traversing the tree level by level and calculating the sum of each level’s nodes. The challenge was to keep track of the largest sums efficiently while avoiding the need to sort all the sums. That’s when I realized that a min-heap could be useful here, as it would allow me to maintain the top k largest sums.

Approach

To solve this problem, I decided to use a Breadth-First Search (BFS) approach because it naturally lends itself to level-order traversal of a binary tree. Here’s how I broke it down:

  1. I start by initializing a min-heap, which will be used to store the sums of node values at each level. The heap is constrained to only store the top k largest sums.
  2. Using BFS, I traverse the tree level by level. For each level, I calculate the sum of all node values.
  3. After calculating the sum for a level, I push it into the min-heap. If the heap size exceeds k, I remove the smallest element. This ensures that only the k largest sums are kept.
  4. Finally, once all levels have been processed, I check if I have at least k sums in the heap. If I do, I return the smallest sum (which is at the root of the min-heap). Otherwise, I return -1 to indicate that the tree doesn’t have k levels.

This approach efficiently maintains the top k largest sums without needing to sort the entire list of sums, which saves both time and space.

Complexity

  • Time complexity: The time complexity is approximately \(O(n \log k)\), where n is the number of nodes in the binary tree. This is because BFS takes \(O(n)\) to traverse all nodes, and each insertion or removal from the heap takes \(O(\log k)\) time.
  • Space complexity: The space complexity is \(O(k)\), as the min-heap stores at most k sums, and the BFS queue holds nodes at each level of the tree. In the worst case, the space used by the queue is proportional to the maximum number of nodes at a level, which is at most \(O(n)\).

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def kthLargestLevelSum(self, root: Optional[TreeNode], k: int) -> int:
        min_heap = []
        self.bfs(root, k, min_heap)
        return min_heap[0] if len(min_heap) >= k else -1

    def bfs(self, root, k, min_heap):
        queue = deque()
        queue.append(root)
        while queue:
            n = len(queue)
            curr_sum = 0
            for _ in range(n):
                node = queue.popleft()
                if node:
                    curr_sum += node.val
                    if node.left:
                        queue.append(node.left)
                    if node.right:
                        queue.append(node.right)
            heapq.heappush(min_heap, curr_sum)
            if len(min_heap) > k:
                heapq.heappop(min_heap)

Editorial

Approach 1: Level Order Traversal + Max Heap

class Solution:
    def kthLargestLevelSum(self, root: TreeNode, k: int) -> int:
        # max heap
        pq = []
        bfs_queue = deque()
        bfs_queue.append(root)

        while bfs_queue:
            # level order traversal
            size = len(bfs_queue)
            level_sum = 0
            for _ in range(size):
                node = bfs_queue.popleft()
                level_sum += node.val
                if node.left:
                    # add left child
                    bfs_queue.append(node.left)
                if node.right:
                    # add right child
                    bfs_queue.append(node.right)

            # Make sum negative to maintain a max heap
            heapq.heappush(pq, -level_sum)

        if len(pq) < k:
            return -1

        for _ in range(k - 1):
            heapq.heappop(pq)

        # Convert sum back to positive
        return -heapq.heappop(pq)

Approach 2: Level Order Traversal + Min Heap

class Solution:
    def kthLargestLevelSum(self, root, k):
        # min heap of size k
        # at the end, top element is kth largest
        pq = []
        bfs_queue = deque()
        bfs_queue.append(root)

        while bfs_queue:
            # level order traversal
            size = len(bfs_queue)
            sum_val = 0
            for _ in range(size):
                popped_node = bfs_queue.popleft()
                sum_val += popped_node.val
                if popped_node.left is not None:
                    # add left child
                    bfs_queue.append(popped_node.left)
                if popped_node.right is not None:
                    # add right child
                    bfs_queue.append(popped_node.right)

            heapq.heappush(pq, sum_val)
            if len(pq) > k:
                # evict top element
                heapq.heappop(pq)
        if len(pq) < k:
            return -1
        return pq[0]

You may also enjoy