Problem of The Day: Cousins in Binary Tree II
Problem Statement
Intuition
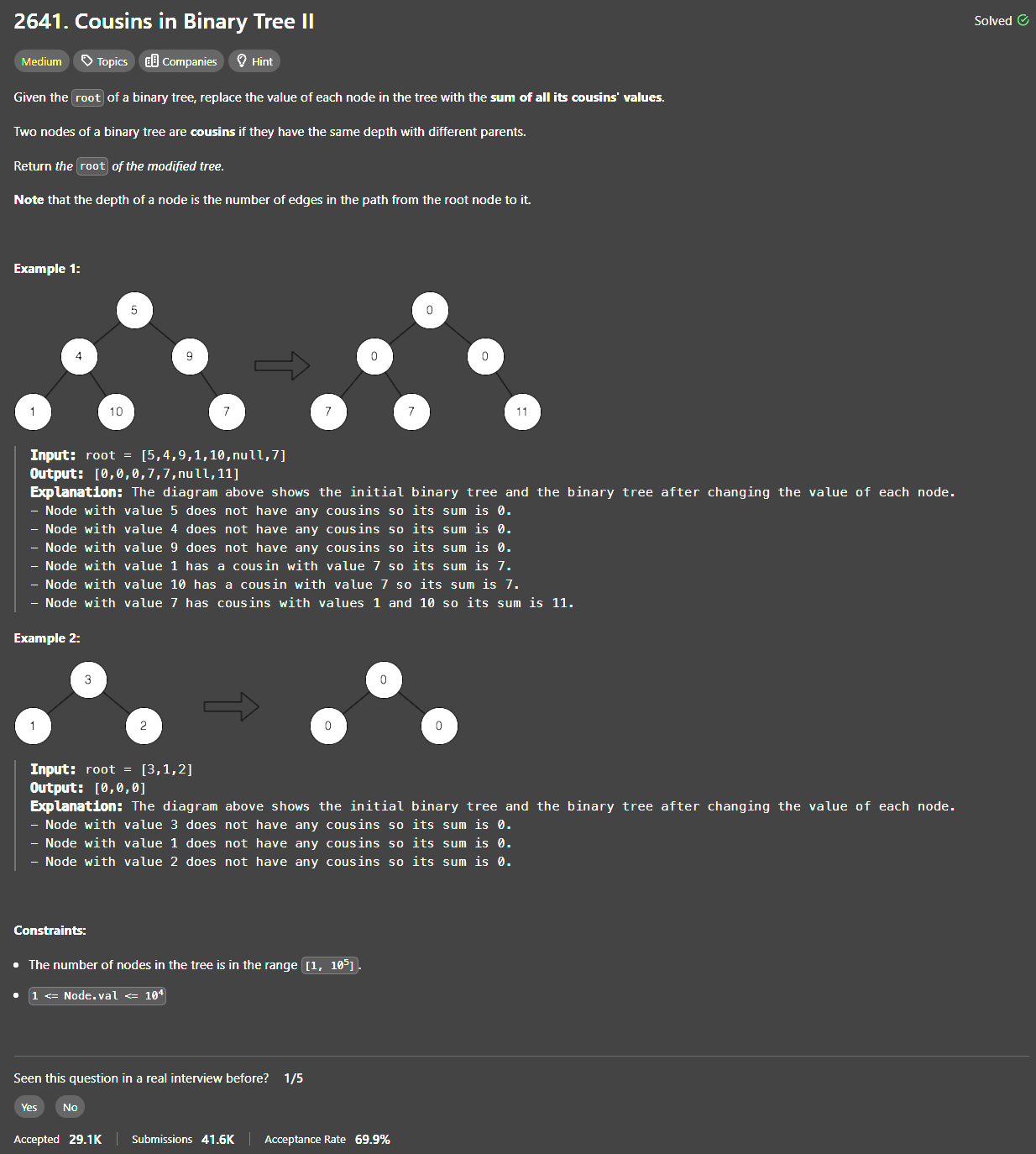
The problem asks us to replace each node’s value with the sum of all its cousins’ values. Cousins are nodes at the same level of the tree, but with different parents.
Initially, the value of each node is independent of its cousin’s value, but we need to collect the total value of all cousin nodes and replace each node’s value with that sum.
Approach
- Level-order traversal: We can traverse the tree level by level using a queue (Breadth-First Search - BFS). This ensures we only look at nodes at the same level.
- Track parents: For each node, we maintain its parent. This helps in identifying which nodes are siblings, so we can exclude them from the sum of cousins.
- Calculate the cousin sum: For each node at a given level, compute the total sum of values for all nodes, and then subtract the sum of values of the siblings for each node. This gives us the sum of the cousins.
- Update values: After calculating the cousin sum, we update each node’s value accordingly.
Complexity
-
Time complexity:
Since we are traversing all the nodes in the tree once, the time complexity is \(O(n)\) where \(n\) is the number of nodes in the tree. -
Space complexity:
The space complexity is also \(O(n)\) because we store the nodes in a queue and maintain dictionaries for sums and parent-child relationships.
Code
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def replaceValueInTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
queue = deque()
queue.append([root, None])
while queue:
n = len(queue)
curr_sum = defaultdict(int)
parents = defaultdict(list)
total_sum = 0
for _ in range(n):
node, parent = queue.popleft()
curr_sum[parent] += node.val
parents[parent].append(node)
total_sum += node.val
if node:
if node.left:
queue.append([node.left, node])
if node.right:
queue.append([node.right, node])
for k, v in curr_sum.items():
sum_all_cousins = total_sum - v
for node in parents[k]:
node.val = sum_all_cousins
return root
Editorial
Approach 1: Two Pass BFS
class Solution:
def replaceValueInTree(self, root):
if not root:
return root
node_queue = deque([root])
level_sums = []
# First BFS: Calculate sum of nodes at each level
while node_queue:
level_sum = 0
level_size = len(node_queue)
for _ in range(level_size):
current_node = node_queue.popleft()
level_sum += current_node.val
if current_node.left:
node_queue.append(current_node.left)
if current_node.right:
node_queue.append(current_node.right)
level_sums.append(level_sum)
# Second BFS: Update each node's value to sum of its cousins
node_queue.append(root)
level_index = 1
root.val = 0 # Root has no cousins
while node_queue:
level_size = len(node_queue)
for _ in range(level_size):
current_node = node_queue.popleft()
sibling_sum = (
current_node.left.val if current_node.left else 0
) + (current_node.right.val if current_node.right else 0)
if current_node.left:
current_node.left.val = (
level_sums[level_index] - sibling_sum
)
node_queue.append(current_node.left)
if current_node.right:
current_node.right.val = (
level_sums[level_index] - sibling_sum
)
node_queue.append(current_node.right)
level_index += 1
return root
Approach 2: Two Pass DFS
class Solution:
def __init__(self):
self.level_sums = [0] * 100000
def replaceValueInTree(self, root):
self._calculate_level_sum(root, 0)
self.replace_value_in_tree_internal(root, 0, 0)
return root
def _calculate_level_sum(self, node, level):
if node is None:
return
self.level_sums[level] += node.val
self._calculate_level_sum(node.left, level + 1)
self._calculate_level_sum(node.right, level + 1)
def replace_value_in_tree_internal(self, node, sibling_sum, level):
if node is None:
return
left_child_val = 0 if node.left is None else node.left.val
right_child_val = 0 if node.right is None else node.right.val
if level == 0 or level == 1:
node.val = 0
else:
node.val = self.level_sums[level] - node.val - sibling_sum
self.replace_value_in_tree_internal(
node.left, right_child_val, level + 1
)
self.replace_value_in_tree_internal(
node.right, left_child_val, level + 1
)
Approach 3: Single BFS with Running Sum
class Solution:
def replaceValueInTree(self, root):
if root is None:
return root
node_queue = deque()
node_queue.append(root)
previous_level_sum = root.val
while node_queue:
level_size = len(node_queue)
current_level_sum = 0
for _ in range(level_size):
current_node = node_queue.popleft()
# Update node value to cousin sum
current_node.val = previous_level_sum - current_node.val
# Calculate sibling sum
sibling_sum = (
0 if current_node.left is None else current_node.left.val
) + (
0 if current_node.right is None else current_node.right.val
)
if current_node.left is not None:
current_level_sum += (
current_node.left.val
) # Accumulate current level sum
current_node.left.val = (
sibling_sum # Update left child's value
)
node_queue.append(
current_node.left
) # Add to queue for next level
if current_node.right is not None:
current_level_sum += (
current_node.right.val
) # Accumulate current level sum
current_node.right.val = (
sibling_sum # Update right child's value
)
node_queue.append(
current_node.right
) # Add to queue for next level
previous_level_sum = current_level_sum # Update previous level sum for next iteration
return root
- time: O(n)
- space: O(n)