Thomas Ngo

Software Engineer

2 minute read

Problem Statement

problem

Intuition

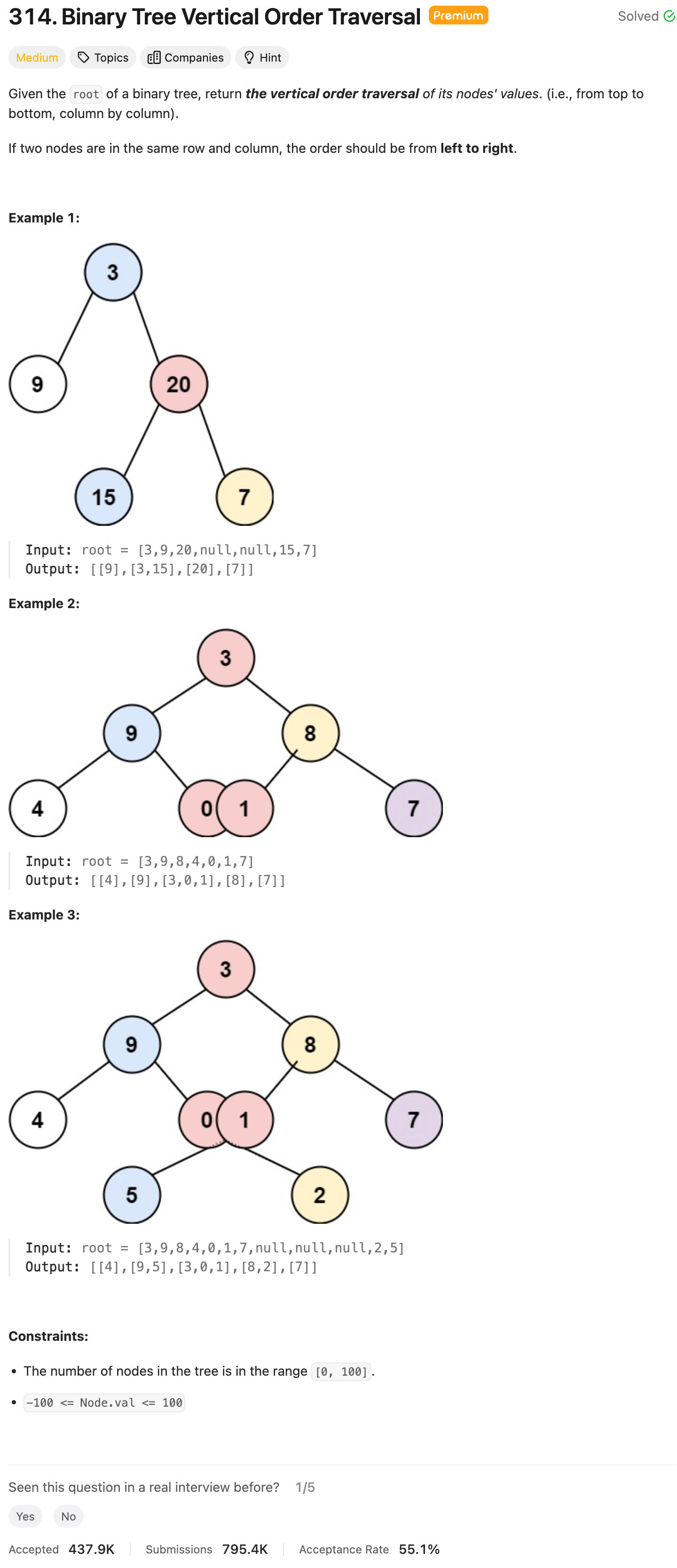
The problem asks to traverse the binary tree in vertical order, which means nodes at the same horizontal distance from the root are grouped together. We can associate each node with a column index starting with 0 for the root, decrementing for the left child, and incrementing for the right child.

Approach

  1. Use a breadth-first search (BFS) traversal to ensure that nodes are processed in the order of their depth.
  2. For each node, keep track of its corresponding column index.
  3. Store nodes belonging to the same column in a dictionary, where the keys are column indices, and values are lists of node values.
  4. Once the traversal is complete, retrieve the values from the dictionary sorted by column index to maintain the correct vertical order.

Complexity

  • Time complexity:
    The time complexity is (O(n \log n)) where (n) is the number of nodes. This is due to the sorting step of the column keys, which takes (O(n \log n)) time.

  • Space complexity:
    The space complexity is (O(n)) as we use a dictionary to store the nodes of each column and a queue to traverse the nodes.

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
from collections import deque, defaultdict
from typing import List, Optional

class Solution:
    def verticalOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if not root:
            return []
        queue = deque([(root, 0)])
        node_dict = defaultdict(list)
        while queue:
            node, col = queue.popleft()
            node_dict[col].append(node.val)
            if node:
                if node.left:
                    queue.append((node.left, col - 1))
                if node.right:
                    queue.append((node.right, col + 1))

        res = []
        cols = sorted(node_dict.keys())
        for col in cols:
            res.append(node_dict[col][:])
        return res

Editorial

Approach 1: Breadth-First Search (BFS)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
from collections import defaultdict
class Solution:
    def verticalOrder(self, root: TreeNode) -> List[List[int]]:
        columnTable = defaultdict(list)
        queue = deque([(root, 0)])

        while queue:
            node, column = queue.popleft()

            if node is not None:
                columnTable[column].append(node.val)

                queue.append((node.left, column - 1))
                queue.append((node.right, column + 1))

        return [columnTable[x] for x in sorted(columnTable.keys())]

Approach 2: BFS without Sorting

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
from collections import defaultdict
class Solution:
    def verticalOrder(self, root: TreeNode) -> List[List[int]]:
        if root is None:
            return []

        columnTable = defaultdict(list)
        min_column = max_column = 0
        queue = deque([(root, 0)])

        while queue:
            node, column = queue.popleft()

            if node is not None:
                columnTable[column].append(node.val)
                min_column = min(min_column, column)
                max_column = max(max_column, column)

                queue.append((node.left, column - 1))
                queue.append((node.right, column + 1))

        return [columnTable[x] for x in range(min_column, max_column + 1)]
  • time: O(n)
  • space: O(n)

Approach 3: Depth-First Search (DFS)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
from collections import defaultdict
class Solution:
    def verticalOrder(self, root: TreeNode) -> List[List[int]]:
        if root is None:
            return []

        columnTable = defaultdict(list)
        min_column = max_column = 0

        def DFS(node, row, column):
            if node is not None:
                nonlocal min_column, max_column
                columnTable[column].append((row, node.val))
                min_column = min(min_column, column)
                max_column = max(max_column, column)

                # preorder DFS
                DFS(node.left, row + 1, column - 1)
                DFS(node.right, row + 1, column + 1)

        DFS(root, 0, 0)

        # order by column and sort by row
        ret = []
        for col in range(min_column, max_column + 1):
            columnTable[col].sort(key=lambda x:x[0])
            colVals = [val for row, val in columnTable[col]]
            ret.append(colVals)

        return ret

You may also enjoy