Problem of The Day: Construct Quad Tree

Problem Statement

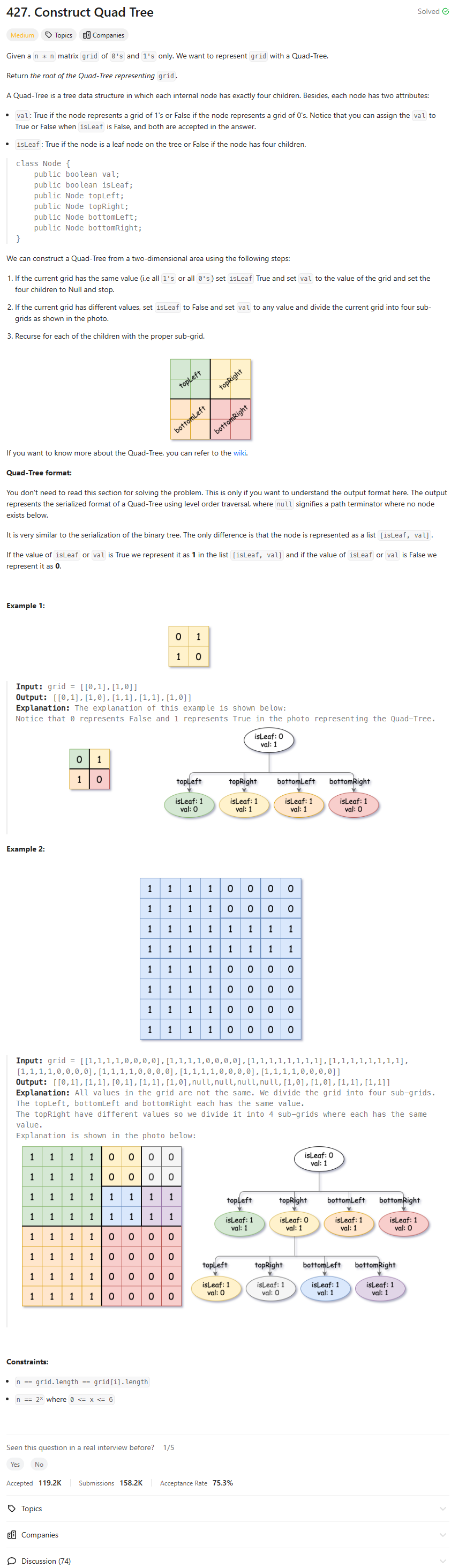
Intuition

The problem seems to involve constructing a quadtree based on the given grid. My initial thought is to recursively divide the grid into quadrants until each quadrant represents a single cell or a leaf node. Then, I can check if all the values in a quadrant are the same. If they are, I can create a leaf node; otherwise, I need to create a non-leaf node with references to its four quadrants.

Approach

I’ll define a recursive helper function to divide the grid into quadrants and check if they contain the same values. If they do, I’ll create a leaf node; otherwise, I’ll create a non-leaf node and recursively call the helper function on its quadrants.

Complexity

• Time complexity: O(n^2)

• Space complexity: O(n^2)

Code

"""
# Definition for a QuadTree node.
class Node:
    def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight):
        self.val = val
        self.isLeaf = isLeaf
        self.topLeft = topLeft
        self.topRight = topRight
        self.bottomLeft = bottomLeft
        self.bottomRight = bottomRight
"""

class Solution:
    def construct(self, grid: List[List[int]]) -> 'Node':
        N = len(grid)

        def areSameValues(rx, cx, ry, cy):
            for row in range(rx, ry):
                for col in range(cx, cy):
                    if grid[rx][cx] != grid[row][col]:
                        return False
            return True


        def helper(rx, cx, ry, cy):
            if rx >= N or cx >= N or rx > ry or cx > cy:
                return None
            if rx == ry and cx == cy:
                return Node(grid[rx][cx], True)

            mid_row = rx + (ry - rx) // 2
            mid_col = cx + (cy - cx) // 2

            topLeft = helper(rx, cx, mid_row, mid_col)
            topRight = helper(rx, mid_col + 1, mid_row, cy)
            bottomLeft = helper(mid_row + 1, cx, ry, mid_col)
            bottomRight = helper(mid_row + 1, mid_col + 1, ry, cy)

            val = topLeft.val and topRight.val and bottomLeft.val and bottomRight.val
            vals = [topLeft.val, topRight.val, bottomLeft.val, bottomRight.val]
            if all(x == vals[0] for x in vals):
                if areSameValues(rx, cx, ry, cy):
                    return Node(grid[rx][cx], True)
            return Node(val, False, topLeft, topRight, bottomLeft, bottomRight)

        return helper(0, 0, N - 1, N - 1)

Editorial Solution

Approach 1: Recursion

class Solution {
public:
    // Returns true if all the values in the matrix are the same; otherwise, false.
    bool sameValue(vector<vector<int>>& grid, int x1, int y1, int length) {
        for (int i = x1; i < x1 + length; i++) {
            for (int j = y1; j < y1 + length; j++)
                if (grid[i][j] != grid[x1][y1])
                    return false;
        }
        return true;
    }

    Node* solve(vector<vector<int>>& grid, int x1, int y1, int length) {
        // Return a leaf node if all values are the same.
        if (sameValue(grid, x1, y1, length)) {
            return new Node(grid[x1][y1], true);
        } else {
            Node* root = new Node(false, false);

            // Recursive call for the four sub-matrices.
            root -> topLeft = solve(grid, x1, y1, length / 2);
            root -> topRight = solve(grid, x1, y1 + length / 2, length / 2);
            root -> bottomLeft = solve(grid, x1 + length / 2, y1, length / 2);
            root -> bottomRight = solve(grid, x1 + length / 2, y1 + length / 2, length / 2);

            return root;
        }
    }

    Node* construct(vector<vector<int>>& grid) {
        return solve(grid, 0, 0, grid.size());
    }
};

Approach 2: Optimized Recursion

class Solution {
public:
    Node* solve(vector<vector<int>>& grid, int x1, int y1, int length) {
        // Return a leaf node if the matrix size is one.
        if (length == 1) {
            return new Node(grid[x1][y1], true);
        }

        // Recursive calls to the four sub-matrices.
        Node* topLeft = solve(grid, x1, y1, length / 2);
        Node* topRight = solve(grid, x1, y1 + length / 2, length / 2);
        Node* bottomLeft = solve(grid, x1 + length / 2, y1, length / 2);
        Node* bottomRight = solve(grid, x1 + length / 2, y1 + length / 2, length / 2);

        // If the four returned nodes are leaf and have the same values
        // Return a leaf node with the same value.
        if (topLeft -> isLeaf && topRight -> isLeaf && bottomLeft -> isLeaf && bottomRight -> isLeaf
           && topLeft -> val == topRight -> val && topRight -> val == bottomLeft -> val
           && bottomLeft -> val == bottomRight -> val) {
            return new Node(topLeft -> val, true);
        }

        // If the four nodes aren't identical, return non-leaf node with corresponding child pointers.
        return new Node(false, false, topLeft, topRight, bottomLeft, bottomRight);
    }

    Node* construct(vector<vector<int>>& grid) {
        return solve(grid, 0, 0, grid.size());
    }
};