Problem of The Day: Diagonal Traverse

Problem Statement

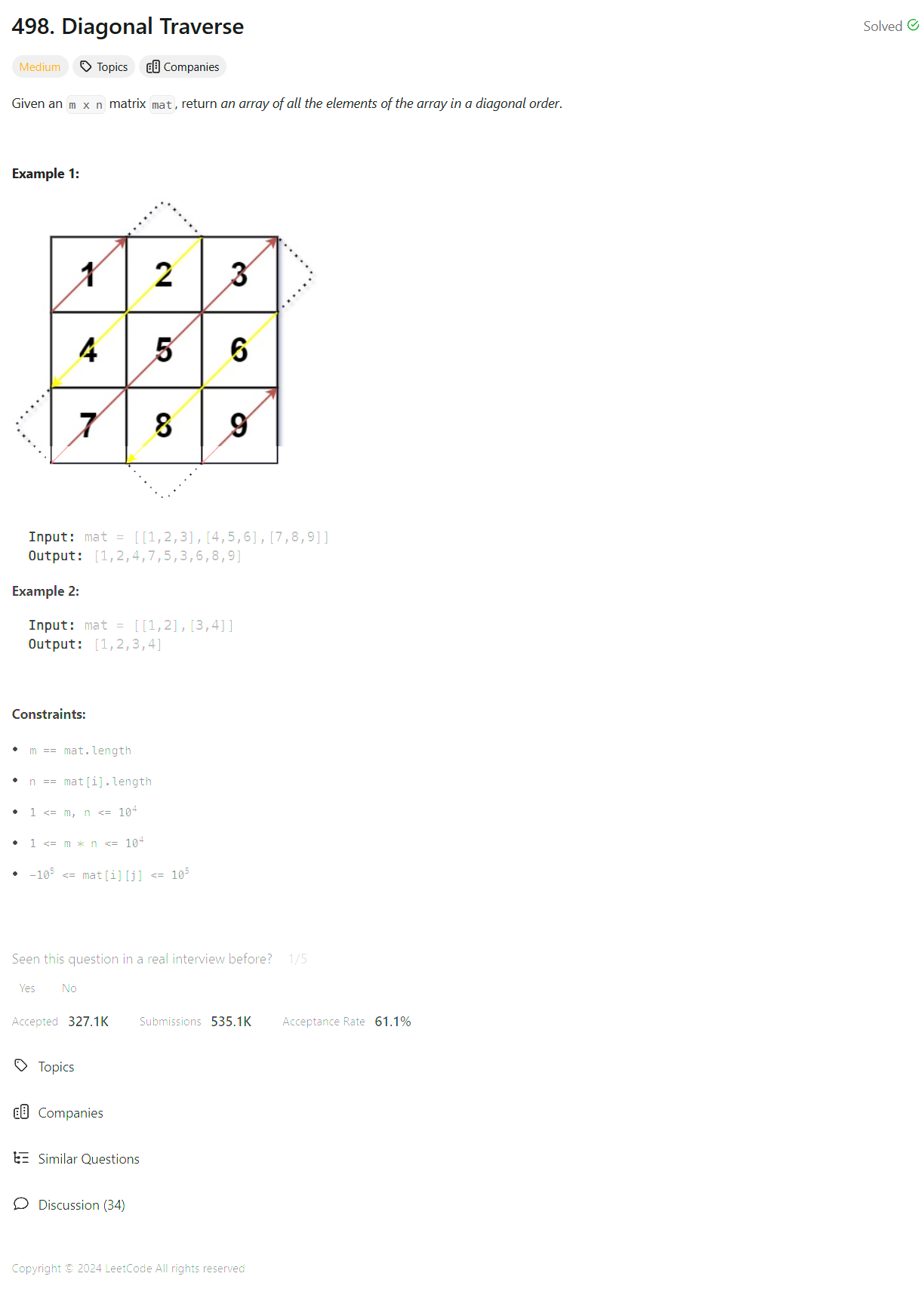
Approach

We traverse the matrix diagonally, extracting each diagonal in two phases:

1. First, starting from each row in the first column.
2. Second, starting from each column in the last row.

For each diagonal, we determine whether to reverse it based on whether we’re moving bottom-to-top or top-to-bottom. We then append the results of each diagonal traversal to our output list.

Complexity

• Time complexity: Since we’re traversing the entire matrix and each element is processed exactly once, the time complexity is \(O(n)\), where n is the total number of elements in the matrix (i.e., rows * columns).

• Space complexity: The space complexity is \(O(n)\), where n is the total number of elements stored in the resulting list.

Code

class Solution:
    def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
        ROWS = len(mat)
        COLS = len(mat[0])
        N = ROWS * COLS
        res = []
        bottom_to_top = True
        for row in range(ROWS):
            curr = []
            r, c = row, 0
            while r >= 0 and c < COLS:
                curr.append(mat[r][c])
                r -= 1
                c += 1
            if not bottom_to_top:
                curr = curr[::-1]
            res.extend(curr)
            bottom_to_top = not bottom_to_top

        for col in range(1, COLS):
            curr = []
            r, c = ROWS - 1, col
            while r >= 0 and c < COLS:
                curr.append(mat[r][c])
                r -= 1
                c += 1
            if not bottom_to_top:
                curr = curr[::-1]
            res.extend(curr)
            bottom_to_top = not bottom_to_top

        return res

Discussion Solution

class Solution:
    def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
        up = True

        i = 0
        j = 0

        m = len(mat)
        n = len(mat[0])
        o = []

        while len(o) < m * n:  # Continue until we've processed all elements
            o.append(mat[i][j])

            if up:
                if i - 1 >= 0 and j + 1 < n:  # Move up diagonally
                    i -= 1
                    j += 1
                else:  # Change direction if boundary is hit
                    up = False
                    if j + 1 < n:  # Move right if possible
                        j += 1
                    else:  # Else move down
                        i += 1
            else:
                if i + 1 < m and j - 1 >= 0:  # Move down diagonally
                    i += 1
                    j -= 1
                else:  # Change direction if boundary is hit
                    up = True
                    if i + 1 < m:  # Move down if possible
                        i += 1
                    else:  # Else move right
                        j += 1

        return o